Pilares de concreto reforçados com aço são usados em grandes construções. Falhas estruturais podem ocorrer em altas temperaturas em função de um incêndio por causa do enfraquecimento do núcleo metálico. Considere um pilar composto com de espessura constituído por um núcleo central de aço (espessura de ) entre duas paredes de concreto com de espessura. O pilar encontra-se em uma temperatura inicial uniforme de Ti = 27°C e é subitamente exposto a produtos de combustão a T∞ = 900°C e nas duas superfícies expostas. A temperatura da vizinhança também é de .
(a) Usando um método implícito de diferenças finitas, com e , determine as temperaturas na superfície exposta do concreto e no centro da placa de aço em . As propriedades do aço são: e As propriedades do concreto são: e. Represente graficamente as temperaturas máxima e mínima do concreto juntamente com as temperaturas máxima e mínima do aço ao longo do .
(b) Repita a parte (a), mas agora leve em conta uma resistência térmica de contato de na interface concreto-aço.
(c) Em t = 10.000 s, o fogo é extinto e as temperaturas da vizinhança e do ambiente retornam a . Usando o mesmo coeficiente de transferência de calor e a mesma efetividade das partes (a) e (b), determine a temperatura máxima do aço e o tempo crítico, no qual ocorre a temperatura máxima no aço para os casos com e sem a resistência térmica de contato. Represente graficamente a temperatura da superfície do concreto, a temperatura do concreto adjacente ao aço e as temperaturas do aço no período .
Passo 1
Vamos lá! Nosso problema pede os gráficos de temperatura, mas antes não vamos esquecer do nosso velho esboço pra facilitar nosso problema.
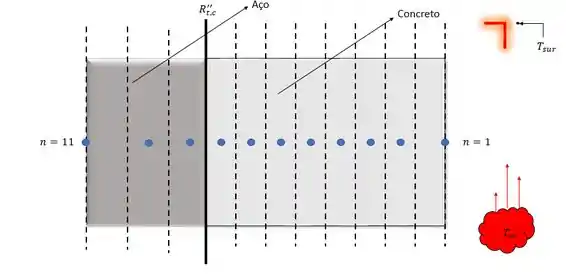
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá! Primeiro que tal fazermos o balanço de energia para todos os nós e seus respectivos volumes de controle:
Nó :
Onde e :
Para os nós :
Para o nó :
Onde , com desprezível:
Para o nó :
Para o nó :
Para o nó :
Passo 3
Agora ele pede o histórico de temperatura para o núcleo de metal e superfície de concreto, para o nó e , normalmente podemos resolver isso em forma de tabela, mas devido à natureza da questão fica melhor fazer com gráfico.
Assim usando o método das diferenças finitas temos.
P.S: Pode desenvolver em qualquer software de sua preferência.
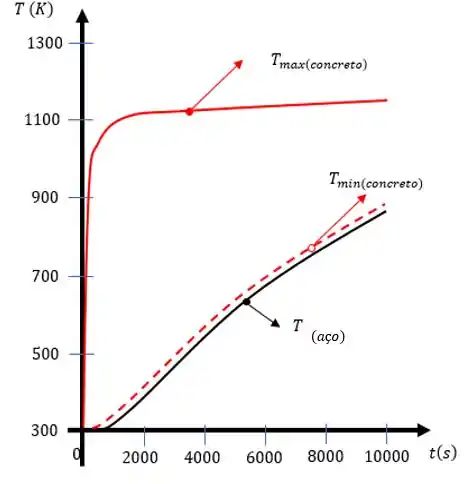
Devido à alta condutividade térmica do metal a temperatura é quase uniforme, entretanto para o concreto devido à baixa condutividade térmica temos uma discrepância entre a temperatura de superfície do concreto e a temperatura interna .
Assim temos que as temperaturas são após :
Passo 4
(b) Adicionando a resistência térmica de contato agora para o nosso problema temos que nosso gráfico fica assim:
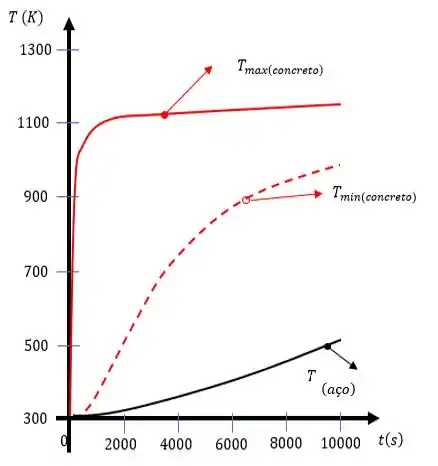
A explicação segue a mesma lógica da letra (a), a discrepância entre a temperatura de superfície e a temperatura interna do concreto, e a temperatura praticamente uniforme do aço.
Entretanto a resistência térmica de contato reduz bastante a quantidade de calor que atravessa o concreto até o aço, assim a temperatura do aço cai drasticamente.
Assim temos que as temperaturas são após :
Passo 5
(c)
Repetindo o passo entretanto agora as temperaturas nodais para , com , considerando o tempo inicial os gráficos vão ficar assim:
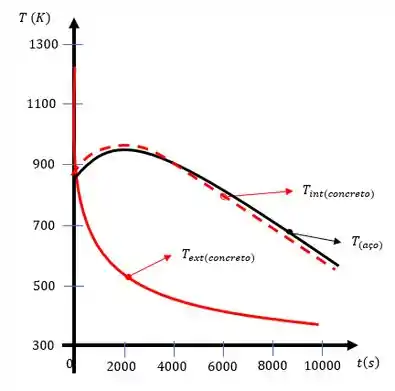
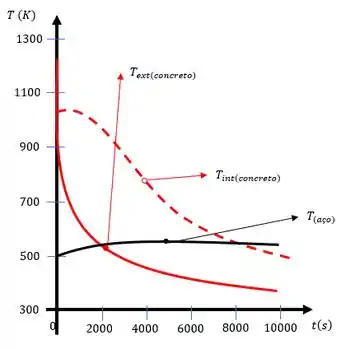
Agora temos que:
Sem resistência de contato
Com resistência de contato
Isso é tudo pessoal! \o/

Resposta
(a) ,
(b),
(c)
Sem resistência de contato
Com resistência de contato