Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 5.Problemas - Ex. 114

114 – Elementos de aquecimento elétrico de pequeno diâmetro dissipando 50W/m são usados para aquecer um prato de cerâmica de condutividade térmica 2W/m.K. A superfície de cima do prato está exposta ao ar ambiente a 30°C com um coeficiente convectivo de 100W/m2.K, enquanto que a superfície de baixo está bem isolado.

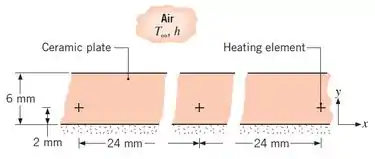
Inicialmente, o prato de cerâmica (α=1,5x10-6m2/s) tem uma temperatura uniforme de 30°C, e repentinamente os elementos de aquecimento elétrico são energizados. Usando o método diferenças finitas implícito, estime o tempo requerido para a diferença entre a temperatura da superfície imediatamente acima do elemento de aquecimento e a temperatura inicial alcançar 95% da diferença de temperatura nas condições de estado estacionário. Use um espaçamento de Δx=6 mm e Δy=2 mm e um incremento de tempo de 1 s.

Passo 1

Vamos começar pegando a expressão do balanço de energia descritizada pelo método de diferenças finitas implícito.

O método implícito para estado estacionário é, pela Eq. 5.94:

T m + 1 , n p + 1 + T m - 1 , n p + 1 - 2 T m . n p + 1 ∆ x 2 + T m , n + 1 p + 1 + T m , n - 1 p + 1 - 2 T m , n p + 1 ∆ y 2 = 0

Que podemos escrever como:

T m + 1 , n p + 1 + T m - 1 , n p + 1 - 2 T m . n p + 1 ∆ y 2 + T m , n + 1 p + 1 + T m , n - 1 p + 1 - 2 T m , n p + 1 ∆ x 2 = 0

Passo 2

Considerando uma distribuição de temperatura uniforme ao longo do eixo y, assim

T m + 1 p + 1 + T m - 1 p + 1 - 2 T m p + 1 ∆ y 2 = 0

T m - 1 p + 1 - 2 T m p + 1 + T m + 1 p + 1 = 0

Para o qual,

T 0 = 30 ℃ = 303   K

Passo 3

O sistema de equações lineares para os 8 nodos é:

- 2 T 1 p + 1 + T 2 p + 1 = - 30

T 1 p + 1 - 2 T 2 p + 1 + T 3 p + 1 = 0

...

T 7 p + 1 - T 8 p + 1 = 0

Agora basta você resolver este sistema linear e encontrar o valor de T1, que será a temperatura imediatamente acima e a diferença de temperatura será

∆ T = T 1 - T 0

Passo 4

Para a condição de regime transiente podemos usar as seguintes expressões:

Para o nodo da superfície, temos que:

1 + 2 F O T 0 p + 1 - 2 F O T 1 p + 1 = 2 α ∆ t k ∆ x q " 0 + T 0 p

Onde, FO é o número de Fourier, que é dado por:

F O = α ∆ t ∆ x 2

F O = ( 1,5 x 10 - 6 ) ( 1 ) 0,006 = 0,00025

Aplicando os valores:

1 + 2 ( 0,00025 ) T 0 p + 1 - 2 ( 0,00025 ) T 1 p + 1 = 2 1,5 x 10 - 6 1 2 0,006 ( 50 ) + T 0 p

1,00 0 5 T 0 p + 1 - 0,00 0 5 T 1 p + 1 = 0,0125 + T 0 p

Para os nodos interiores podemos usar a eq. 5.97 do Incropera é aplicada para nodos interiores com o método de diferenças finitas implícito. Assim, para os nodos de 1 até 8:

1 + 2 F O T m p + 1 - F O T m - 1 p + 1 + T m + 1 p + 1 = T m p

Substituindo, vamos chegar que:

- 0,0005 T m - 1 p + 1 + 1,0005 T m p + 1 - 0,0005 T m + 1 p + 1 = T m p

Essa é eq. para cada nodo m interior de 1 até 7

Passo 5

Assim, vamos ter que resolver o seguinte sistema linear:

- T 6 p + 1 + 4 T 7 p + 1 - T 8 p + 1 = 2 T 7 p

- T 5 p + 1 + 4 T 6 p + 1 - T 7 p + 1 = 2 T 6 p

...

- T 0 p + 1 + 4 T 1 p + 1 - T 2 p + 1 = 2 T 1 p

1 , 0005 T 0 p + 1 - 0,0005 T 1 p + 1 = 0,0125 + T 0 p

Vamos considerar que no passo de tempo de p = 0, isto é, no tempo inicial, todas as temperaturas são iguais a 30ºC

T 0 0 = T 1 0 = T 2 0 = … = T 8 0 = 3 0 ℃

Logo, para você determinar o tempo requerido para atingir 95% da diferença de temperatura, você deve encontrar a temperatura correspondente que fará com que a diferença entre as temperaturas seja 95% da diferença de temperatura do estado estacionário, e você deve verificar em qual valor de p, ou seja, em qual passo p, a temperatura atingiu esse valor. Com o valor de p basta você aplicar a relação matemática seguinte e encontrar o tempo requerido:

t = p ∆ t

Resposta

Nodo interior m:

- 0,0005 T m - 1 p + 1 + 1,0005 T m p + 1 - 0,0005 T m + 1 p + 1 = T m p

Nodo exterior, m=0:

1,0005 T 0 p + 1 - 0,0005 T 1 p + 1 = 0,0125 + T 0 p

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com referência ao Comentário 4 do Exemplo 5.12 , analise a súbita exposição da superfície a uma grande vizinhança, a uma temperatura elevada ( T v i z ) , e a condições de convecção ( T ∞ ,h ) .(a) De
Considere a operação de colagem descrita no Problema 3.115 , que foi analisada sob condições de regime estacionário. Agora, entretanto, o laser será usado para aquecer a película durante um período de
Uma barra com 10m m de diâmetro e 250m m de comprimento tem uma de suas extremidades mantida a 100 ° C . Na superfície da barra há transferência de calor por convecção natural com o ar ambiente a 25 °
Resolva pelo método de diferenças finitas, o PVC y ' ' + 2 y ' + y = x y ( 0 ) = 2 y ( 1 ) = 0 usando h = 0.25.
Formule, por diferenças finitas, sistemas de equações cuja solução aproxime a solução dos seguintes problemas de contorno: y ' ' = y s e n ( y ) + t y y ( 0 ) = 1 y ( 1 ) = 5 y ' ' = 2 y + y 3 - t y (