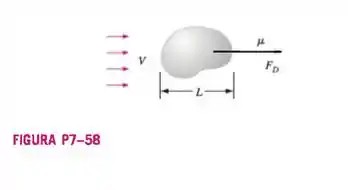
Quando pequenas partículas de aerossol ou microorganismos se movem através do ar ou da água, o número de Reynolds é muito pequeno . Tais escoamentos são chamados de escoamentos lentos. O arrasto aerodinâmico de um objeto no escoamento lento é uma função apenas de sua velocidade , de alguma escala de comprimento característica do objeto e da viscosidade do fluido . (Figura P7-58). Use a análise dimensional para gerar uma relação para como função das variáveis independentes.

Agora a gente precisa listar as dimensões primárias de cada parâmetro!

Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões e , então podemos considerar:

Teorema de Pi de Buckingham:

O a gente já tinha achado no Passo 1, lá vimos que !

Substituindo:

Nesse caso o número de grupos esperado é igual a 1. Então vamos atrás dele!!

Antes de começar a precisamos decidir quais vão ser os parâmetros repetidos.

Pra relembrar nossos parâmetros:

Como não podemos usar , já que ele é um parâmetro dependente, resta pra a gente .

Agora sim, vamos encontrar o nosso grupo !!

Organizando os nossos parâmetros a gente fica com:

Escrevendo suas dimensões básicas:

Agora equacionando:

Massa:

Comprimento:

Tempo:

Logo:

Substituindo , e , temos:

Organizando:

Agora é aquele momento que a gente escreve a relação entre os grupos , mas aqui a gente só tem um grupo ! Como ele não vai ser uma função de nada, logo a gente espera que ele seja igual a uma constante!