Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 45

A velocidade do ar no duto de um sistema de aquecimento deve ser medida por uma sonda estática de Pitot inserida no duto paralelamente ao escoamento. Se a altura diferencial entre as colunas d'água conectadas as duas saídas da sonda é de 2,4   c m , determine (a) a velocidade de escoamento e (b) a elevação da pressão na ponta da sonda. A temperatura e pressão do ar no duto são de 45 ° C e 98   k P a , respectivamente.

Passo 1

Bom, aqui nós temos duas colunas d’agua conectadas a um duto, em que a sonda de Pitot mede a velocidade de ar. Assim, vamos encontrar a velocidade de escoamento e a elevação da pressão na ponta da sonda.

Em forma de diagrama, temos:

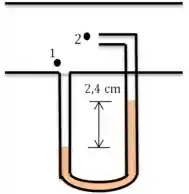
Passo 2

Nós iremos levar em consideração dois pontos, o ponto 1 é distanciado do ponto 2 o qual se localiza na ponta do tubo de Pitot e é usado para medir o ponto de estagnação. Observe:

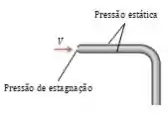
Esse ponto de estagnação é onde o fluido para totalmente, ou seja, V 2 = 0 e z 1 = z 2 . Substituindo isso na equação do nosso amigo Bernou:

P 1 ρ g + V 1 2 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2

P 1 ρ g + V 1 2 2 g = P 2 ρ g

Isolamos a velocidade:

V 1 = 2 ( P 2 - P 1 ) ρ

Passo 3

Temos as referências para calcular a densidade do ar, para essa pressão e temperatura a constante do ar é R = 0,287   k P a   m 3 k g K :

ρ = P R T

ρ = 98   k P a 0,287   k P a   m 3 k g K × 45 + 273 K = 1,07 k g m 3

A diferença de pressão na ponta da sonda pode ser calculada por:

P 2 - P 1 = ρ g h

P 2 - P 1 = 1000 k g m 3 × 9,8 m s 2 × 0,024   m

P 2 - P 1 = 235   P a

Utilizando a equação do Passo 2 e substituindo os dados do nosso enunciado:

V 1 = 2 × ( 235   P a ) 1,07 k g m 3 = 20,9   m / s

Prontinho!!

Resposta

(a) V 1 = 20,9   m / s

(b) P 2 - P 1 = 235   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados: H p 2,3 = 2m ; A 3 = 20c m 2 ; A 2 = 1c m 2 ; H p 0,1 = 0,8m ; η B = 70 % . Determinar:a vazão ( L / s ) ;a área da seção 1 c m 2 ;a potência fornecida pela bomba ao fluido.
Num carburador, a velocidade do ar na garganta do Venturi é 120m / s . O diâmetro da garganta é 25m m . O tubo principal de admissão de gasolina tem um diâmetro de 1,15m m e o reservatório de gasolina
A pressão no ponto S do sifão da figura não deve cair abaixo de 25k P a( a b s ) . Desprezando as perdas, determinar:A velocidade do fluido;A máxima altura do ponto S em relação ao ponto A ; p a t m =
Na extremidade de uma tubulação de diâmetro D , acha-se instalado um bocal que lança um jato de água na atmosfera com diâmetro de 2c m . O manômetro metálico registra uma pressão de 20k P a e a água s
Sabendo que a potência da bomba é 3k W , seu rendimento 75 % e que o escoamento é de 1 para 2 , determinar:A vazão;A carga manométrica da bomba;A pressão do gás.Dados: H p 1,2 = H 5,6 = 1,5m ; H p 3,4