Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 24
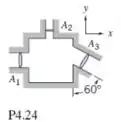
Um fluido, com massa específica de 1.040 kg/m3, flui em regime permanente através da caixa retangular mostrada. Dados , , , e , determine a velocidade 3.
Passo 1
Fala aí! Nesse problema temos um fluxo através da caixa… O objetivo é encontrar a velocidade na estação 3. Para isso, utilizaremos a equação:
Precisamos fazer as seguintes considerações: fluxo constante, incompressível e uniforme.
Passo 2
Então para a caixa, vamos ter:
Observe que os vetores indicam que o fluxo está dentro no local 1 e fora no local 2. Logo, assumimos vazão no local 3:
Pela geometria, temos:
Logo,
Resposta
Exercícios de Livros Relacionados
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. Dados: Seção ( 1 ) : v = 4 1 - r R 2 ; Q 1 = 2m 3 / s ; ρ 1 = 0,6k g / m 3 Seção ( 2 ) : v = 9 1 - r 0,4 ; ρ 2 = 1,2k g
O insuflador de ar da figura gera 16.200m 3 / h na seção ( 0 ) com uma velocidade média de 9,23m / s . Foram medidas as temperaturas nas seções 0 ,( 1 ) e ( 2 ) , sendo, respectivamente, t 0 = 17 ° C
O campo de velocidades de um escoamento bidimensional é dado por v x = 3 + 2 x y + 4 t 2 , v y = x y 2 + 3 t . Determinar os módulos da velocidade e aceleração no ponto 2 ; 1 no instante t = 5s .
UM escoamento é definido pelo campo de velocidades v x = 2 ( 1 + t ) , v y = 3 1 + t , v z = 4 1 + t . Qual é o módulo da velocidade no ponto 3 ; 1 ; 4 no instante t = 2s ? Qual é o módulo da aceleraç
Exercício anterior com v x = 0 , v y = 3 x y e ponto de coordenadas ( 2 ; 2 ) .