Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 54

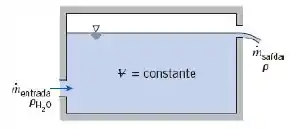
Um tanque de volume fixo contém salmoura com massa específica inicial, ρ i , maior que a da água. Água pura entra no tanque em regime permanente e misturasse perfeitamente com a salmoura. O nível do líquido no tanque permanece constante. Deduza expressões para (a) a taxa de variação da massa específica da mistura líquida no tanque, e (b) o tempo requerido para que a massa específica dessa mistura atinja o valor ρ f , sendo ρ i > ρ f > ρ H 2 O .

Passo 1

Podemos aplicar a equação da conservação de massa ao volume de controle. Assim obtemos que:

∂ ∂ t ∫ V C   ρ d ∀ + ∫ S C   ρ V → ⋅ d A → = 0

Podemos assumir as seguintes considerações:

∀ t a n q u e = c o n s t a n t e .

Fluxo uniforme.

Passo 2

a) Como o volume do tanque é constante, equação da conservação de massa fica da seguinte forma:

∂ ∂ t ρ ∀ - ρ H 2 O V A + ρ V A = 0

∀ ∂ ρ ∂ t = ρ H 2 O V A - ρ V A

∂ ρ ∂ t = ρ H 2 O V A - ρ V A ∀

Portanto, a taxa de variação da densidade do líquido é  ∂ ρ ∂ t = ρ H 2 O V A - ρ V A ∀ .

Passo 3

b) Para encontrar o tempo requerido para que a massa específica dessa mistura atinja o valor ρ f , podemos usar a equação encontrado no passo anterior.

∂ ρ ∂ t = ρ H 2 O V A - ρ V A ∀

Podemos separar as variáveis ​​para obtemos:

∂ ρ ∂ t = V A ρ H 2 O - ρ ∀

1 ρ H 2 O - ρ ∂ ρ = V A ∀ ∂ t

Agora, aplicamos a integração no lado esquerdo da equação entre os limites da densidade inicial  ρ i e a densidade final ρ f , e a integral do lado direito de 0 a t .

∫ ρ i ρ f 1 ρ H 2 O - ρ ∂ ρ = ∫ 0 t V A ∀ ∂ t

ln ⁡ ρ H 2 O - ρ ρ i ρ f = V A ∀ t 0 t

ln ⁡ ρ H 2 O - ρ f - ln ⁡ ρ H 2 O - ρ i = V A ∀ t

ln ⁡ ρ H 2 O - ρ f ρ H 2 O - ρ i = V A ∀ t

t = ∀ V A ln ⁡ ρ H 2 O - ρ f ρ H 2 O - ρ i

Portanto, o tempo necessário para a densidade atingir  ρ f é t = ∀ V A ln ⁡ ρ H 2 O - ρ f ρ H 2 O - ρ i .

Resposta

∂ ρ ∂ t = ρ H 2 O V A - ρ V A ∀

t = ∀ V A ln ⁡ ρ H 2 O - ρ f ρ H 2 O - ρ i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O insuflador de ar da figura gera 16.200m 3 / h na seção ( 0 ) com uma velocidade média de 9,23m / s . Foram medidas as temperaturas nas seções 0 ,( 1 ) e ( 2 ) , sendo, respectivamente, t 0 = 17 ° C
O campo de velocidades de um escoamento bidimensional é dado por v x = 3 + 2 x y + 4 t 2 , v y = x y 2 + 3 t . Determinar os módulos da velocidade e aceleração no ponto 2 ; 1 no instante t = 5s .
UM escoamento é definido pelo campo de velocidades v x = 2 ( 1 + t ) , v y = 3 1 + t , v z = 4 1 + t . Qual é o módulo da velocidade no ponto 3 ; 1 ; 4 no instante t = 2s ? Qual é o módulo da aceleraç
Exercício anterior com v x = 0 , v y = 3 x y e ponto de coordenadas ( 2 ; 2 ) .
Exercício anterior com v x = - 2 y , v y = 3 x e ponto de coordenadas ( 2 ; 3 ) .