Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 11

Deduza a Equação ( 4.12 b )   para coordenadas cilíndricas considerando o escoamento de um fluido incompressível para dentro e para fora do volume de controle elementar da Figura 4.2 .

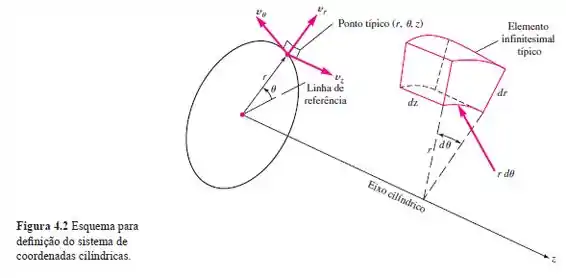
Passo 1

E aí, tudo bem? Bora matar essa questão, mas antes vamos fazer um esqueminha!

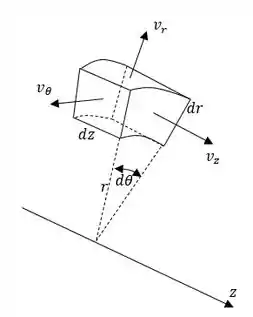
Para o volume de controle no nosso esqueminha, vamos ter a seguinte situação:

∂ ρ ∂ t d v o l + Σ d m ˙ s a i - Σ d m ˙ e n t r a = 0

∂ ρ ∂ t r + d r 2 d θ d r d z + ρ v r r d z d θ + ∂ ∂ r ρ v r d r r + d r d z d θ + ρ v θ d z d r

+ ∂ ∂ θ ρ v θ d θ d z d r + ρ v z r + d r 2 d θ d r + ∂ ∂ z ρ v z r + d r 2 d θ d r

- ρ v r r d z d θ - ρ v θ d z d r - ρ v z r + d r 2 d θ d r = 0

Vamos cancelar as variáveis, tais como d θ , d r , d z e de quarta ordem, tais como d r d θ d z d r , após isso vamos dividir por r :

∂ ρ ∂ t r + 0 + ∂ ∂ r ρ v r r + 0 + ∂ ∂ θ ρ v θ + 0 + ∂ ∂ z ρ v z r - 0 - 0 - 0 = 0

Dividindo tudo por r :

∂ ρ ∂ t + 1 r ∂ ∂ r ρ r v r + 1 r ∂ ∂ θ ρ v θ + ∂ ∂ z ρ v z = 0

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

Demonstração vide passo-a-passo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente x da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é u = A e x / bcos ⁡ ( y / b ) , em que A = 10m / s e b = 5m e x e y são medidos em metros.
A componente x da velocidade em um campo de escoamento em regime permanente e incompressível no plano x y é v = 2 x y x 2 + y 2 2 Mostre que a expressão mais simples para a componente x da velocidade
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação senoidal de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U , na
Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento tridimensional incompressível?a) u = 2 y 2 + 2 x z ; v = - 2 y z + 6 x 2 y z ; w = 3 x 2 z 2 + x 3 y 4 b) u = x y z
Uma aproximação grosseira para a componente x da velocidade em uma camada-limite laminar e encompressível é uma variação linear de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,