Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 173

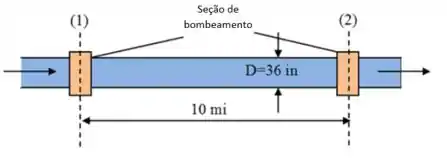
A 36-in-diameter pipeline carries oil (SG 5 0.89) at

1 million barrels per day (bbl/day) (1 bbl 5 42 U.S. gal).

The friction head loss is 13 ft/1000 ft of pipe. It is planned

to place pumping stations every 10 mi along the pipe.

Estimate the horsepower that must be delivered to the oil

by each pump.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

A figura mostrando a porção do tubo

Passo 2

Encontre perda total de carga,

h f   = 13 1000 × 10 m i   = 0.13 m i   = 0.13 m i × 5280 f t 1 m i   = 686.4 f t

Aplicar a equação de Bernoulli entre duas estações de bombeamento,

p 1 ρ oil  g + V 1 2 2 g + z 1 = p 2 ρ oil  g + V 2 2 2 g + z 2 + h f . . . ( 1 )

Aqui, p 1 é a pressão que atua na seção (1), p 2 é a pressão que atua na seção (2), ρ ó leo   é a densidade do fluido, V é a velocidade do fluido, g é a aceleração devido à gravidade e, z é a altura do fluido.

Passo 3

A velocidade e o altitude de ambas as seções são iguais. Reorganize a equação (1) para a mudança de pressão como mostrado:

p 1 ρ ó leo   g = p 2 ρ oil  g + h f p 1 - p 2 ρ oil  g = h f p 1 - p 2 = h f ρ ó leo   g Δ p = h f ( S G ) ρ á gua   g

Substituindo valores

Δ p   = h f ( S G ) ρ á gua   g   = 686.4 × 0.89 × 1.94 × 32.2   = 38161.45 l b f / f t 2

Passo 4

Encontre a taxa de fluxo de volume em termos de f t 3 / s ,

Q   = 1000000   barris   /   dia   = 1000000   barris   1   dia   × 5.615 f t 3 1   barris   × 1   dia   24 × 3600   s   = 64.99 f t 3 / s

Encontre a energia necessária,

P   = Q Δ p   = 64.99 f t 3 / s × 38161.45 l b f / f t 2   = 2480112.636 f t 2 ⋅ l b f / s   = 2480112.636 f t 2 ⋅ l b f / s × 1.3558   W f t 2 ⋅ l b f / s × 1 h p 745.7   W   = 4509.24 h p

Portanto, a potência fornecida ao óleo por cada bomba é 4509.24 h p .

Resposta

P = 4509.24 h p

Exercícios de Livros Relacionados

Um tubo convergente-divergente, chamado Venturi, desenvolve um escoamento de baixa pressão na garganta capaz de aspirar fluido para cima de um reservatório, como na Figura P3.161. Aplicando a equação
Um medidor Venturi, mostrado na Figura P3.165, tem uma redução de seção cuidadosamente projetada cuja diferença de pressão é uma medida da vazão no tubo. Aplicando a equação de Bernoulli para escoamen
Na Figura P3.164, o jato aberto de água a 20°C sai de um bocal para o ar ao nível do mar e atinge um tubo de estagnação, como mostra a figura. Se a pressão na linha de centro na seção 1 é 110 kPa e as
O tanque de água cilíndrico na Figura P3.159 está sendo abastecido com uma vazão volumétrica Q 1 = 3,79 L m i n , enquanto a água é também drenada por um furo na parte inferior de diâmetro d = 6m m .
A forma incompressível da equação de Bernoulli, Equação (3.77), é precisa apenas para escoamentos com números de Mach menores que 0,3, aproximadamente. Para velocidades mais altas, a variação de densi