Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 69
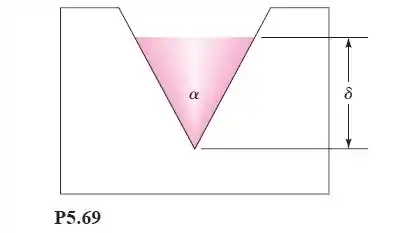
Um dispositivo simples para medir vazão em cursos d’água e canais é um vertedouro triangular de ângulo α, construído na parede de uma barragem, como mostra a Figura P5.69. A vazão volumétrica Q depende somente de α, da aceleração da gravidade g e da altura δ da superfície da água a montante acima do vértice do triângulo. Os testes com um modelo do vertedouro triangular, de ângulo , forneceu os seguintes dados de vazão:
(a) Encontre uma correlação adimensional para os dados.
(b) Use os dados do modelo para prever a vazão de um protótipo de vertedouro triangular, também de ângulo , quando a altura a montante for de 3,2 m.
Passo 1
Bora pra mais uma!
- De , note que que . Daí, a relação apropriada para seu adimensional é:
- O coeficiente médio é: , como o ângulo manteve-se igual, podemos prever o fluxo do protótipo:
Vamos então recalcular os dados com constante:
Resposta
Exercícios de Livros Relacionados
Ao estudar o transporte de areia pelas ondas oceânicas, A. Shields, em 1936, postulou que o limiar de tensão de cisalhamento τ induzida pelas ondas no fundo, requerida para mover partículas, depende d
Quando um fluido em um tubo é acelerado linearmente a partir do repouso, ele começa a escoar como um escoamento laminar e em seguida sofre uma transição para a turbulência em um instante t t r que dep
Adimensionalize a equação da energia (4.75) e suas condições de contorno (4.62), (4.63) e (4.70) definindo T * = T / T 0 , em que T 0 é uma temperatura de entrada, considerada constante. Use outras va
Uma turbina de fluxo axial tem um torque de saída M que é proporcional à vazão volumétrica Q e também depende da massa específica ρ , do diâmetro D do rotor e da velocidade angular de rotação Ω . Como
Quando submetia a uma perturbação, uma boia de flutuação irá oscilar para cima e para baixo a uma frequência f. Admita que essa frequência varia com a massa m da boia, com o diâmetro d da linha de águ