A energia transferida da câmara anterior do olho através da córnea varia consideravelmente dependendo do uso ou não de uma lente de contato. Trate o olho como um sistema esférico e suponha o sistema em regime estacionário. O coeficiente convectivo permanece inalterado com ou sem a presença da lente de contato. A córnea e a lente cobrem um terço da área da superfície esférica.

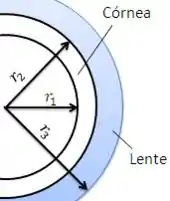
Os valores dos parâmetros que representam essa situação são os seguintes:

(a) Construa os circuitos térmicos, identificando todos os potenciais e escoamentos para os sistemas com e sem a lente de contato. Escreva as resistências em termos dos parâmetros apropriados.

(b) Determine a perda de calor da câmara anterior, com e sem a lente de contato.

(c) Discuta a implicação de seus resultados.

Continuando o item (a) vamos agora desenhar o circuito térmico considerando a presença das lentes. Neste caso, teremos a adição de uma resistência à condução na lente, além das outras três resistências que também estavam presentes no caso anterior (convecção interna e externa e condução na córnea). Então, nossas resistências serão:

E as resistências condutivas serão:

E

O circuito de resistências para o caso em que há lentes é:

Vamos agora para o item (b). Devemos determinar a perda de calor para cada situação. Começando pela situação sem as lentes de contato, a resistência total é:

Então a perda de calor para o primeiro caso é:

Vamos agora para a condição em que há lentes. Nesta condição a resistência equivalente é:

E a perda de calor para este sistema é:

O item (c) pede avaliar o resultado no item (b). Podemos ver que a adição das lentes de contato causa um aumento da taxa de transferência de calor. A explicação para isso é que o raio 3 é menor que o raio crítico para o sistema.