Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 46

Ar entra em um tanque através de uma área de 0,018   m 2 com velocidade de 4,6   m / s e massa específica de 15,5   k g / m 3 . Ar sai com uma velocidade de 1,5   m / s e uma massa específica igual àquela no tanque. A massa específica inicial do ar no tanque é 10,3   k g / m 3 . O volume total do tanque é 0,6   m 3 e a área de saída é 0,04   m 2 . Determine a taxa de variação inicial da massa específica do ar no tanque.

Passo 1

Dados fornecidos:

O ar entra no tanque com as seguintes condições:

Área de entrada  A 1 = 0,018   m 2 .

Velocidade de entrada V 1 = 4,6   m / s . 

Densidade na entrada ρ 1 = 15,5   k g / m 3 . 

O ar sai do tanque com as seguintes condições:

Área de saída A 2 = 0,04   m 2 . 

Velocidade de saída V 2 = 1,5   m / s . 

Densidade na saída ρ 2 = ρ  

Parâmetros do tanque:

Densidade inicial do ar no tanque   ρ = 10,3   k g / m 3 . 

Volume total do tanque V t = 0,6   m 3 . 

Passo 2

Podemos fazer um esboço do volume de controle da seguinte maneira:

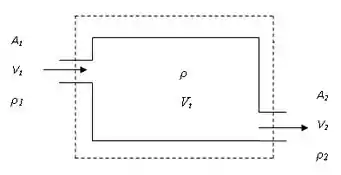
A área pontilhada representa o volume de controle.

Passo 3

Agora, nós vamos aplicar a equação da conservação de massa no volume de controle. Usando a equação básica, temos:

∂ ∂ t ∫ V C   ρ d ∀ + ∫ S C   ρ V → ⋅ d A → = 0

Premissas:

1. Como a densidade é uniforme no tanque. Assim:

∂ ∂ t ∫ V C   ρ d ∀ = ∂ ∂ t ρ ∀

2. O fluxo é uniforme na entrada e na saída. Portanto:

∫ S C   ρ V → ⋅ d A → = ρ 1 V 1 → ⋅ A 1 → + ρ 2 V 2 → ⋅ A 2 →

Substituindo na equação temos:

∂ ∂ t ρ ∀ + ρ 1 V 1 → ⋅ A 1 → + ρ 2 V 2 → ⋅ A 2 → = 0

Como o volume não varia com o tempo, e realizando o produtor vetorial, temos:

∀ ∂ ∂ t ρ - ρ 1 V 1 A 1 + ρ 2 V 2 A 2 = 0

∀ ∂ ∂ t ρ = ρ 1 V 1 A 1 - ρ 2 V 2 A 2

∂ ∂ t ρ = ρ 1 V 1 A 1 - ρ 2 V 2 A 2 ∀

Passo 4

Para encontrar a taxa de variação inicial da massa específica do ar no tanque, basta substituirmos os termos da equação pelos valores conhecidos. Assim temos:

∂ ρ ∂ t = 15,5   k g / m 3 4,6   m / s 0,018   m 2 - 10,3   k g / m 3 1,5   m / s 0,04   m 2 0,6   m 3

∂ ρ ∂ t = 1,109   k g / m 3 ⋅ s

Portanto, a taxa inicial de mudança de densidade no tanque é  1,109   k g / m 3 ⋅ s .

Resposta

∂ ρ ∂ t = 1,109 k g m 3 ⋅ s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A área sombreada mostrada está em um escoamento onde o campo de velocidade é dado por V =a x î=b y ĵ î ĵ; a=b=1s - 1 e as coordenadas são medidas em metros. Avalie a vazão volumétrica e o fluxo de qua
Para o escoamento do Problema 4.17, obtenha uma expressão para o fluxo de energia cinética, ∫ ( V 2 2 )ρ V → d A → , através da seção normal ao eixo do tubo.
A ducha de um chuveiro alimentado por um tubo de água com diâmetro interno de 19,05 mm consiste em 50 bocais de diâmetros internos de 0,79 mm. Considerando uma vazão de 1,39× 10 - 4 m 3 s , qual é a v
Um agricultor de arroz necessita encher de água uma área de plantio de 150 m × 400 m, com uma profundidade de 7,5 cm em 1 h. Quantos tubos de suprimento de água com 37,5 cm de diâmetro são necessários
Considere o escoamento incompressível e permanente através do dispositivo mostrado. Determine o módulo e o sentido da vazão volumétrica através da porta 3.