Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 2
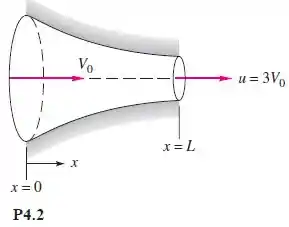
O escoamento pelo bocal convergente da Figura pode ser aproximado por uma distribuição de velocidades unidimensional
(a) Encontre uma expressão geral para a aceleração do fluido no bocal. (b) Para o caso específico e , calcule a aceleração, em g’s, na entrada e na saída.
Passo 1
E aí, tudo bem? Bora matar essa questão rapidinho!
a)
Nosso campo de velocidade é unidimensional o que facilita muito nossas continhas. Heheagora vamos só derivar o campo de velocidade como fizemos na questão anterior!
Como não temos componentes dependentes do tempo:
Passo 2
b)
Agora para matarmos essa de vez, só precisamos substituir os valores na formula que encontramos!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
a)
b)
Exercícios de Livros Relacionados
A two-dimensional, incompressible flow has the velocitycomponents u 5 4y and v 5 2x. (a) Find the accelerationcomponents. (b) Is the vector acceleration radial? (c) Sketcha few streamlines in the firs
For laminar flow between parallel plates (see Fig. 4.12b),the flow is two-dimensional (υ ? 0) if the walls areporous. A special case solution is u 5 (A 2 Bx)(h2 2 y2),where A and B are constants. (a)
In an axisymmetric flow, nothing varies with θ, and theonly nonzero velocities are υr and υz (see Fig. 4.2). If theflow is steady and incompressible and υz 5 Bz, where B isconstant, find the most gene
Deslocamento de inteiros à direita. Escreva um
For an incompressible plane flow in polar coordinates, weare givenυr 5 r3 cos θ 1 r2 sin θFind the appropriate form of circumferential velocity forwhich continuity is satisfied.