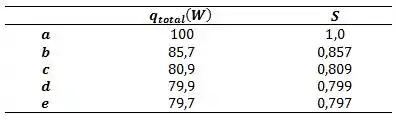
O fator de forma para a condução através do canto formado por duas paredes adjacentes, com , sendo D e L a profundidade e a espessura da parede, respectivamente, é mostrado na Tabela 4.1. O elemento simétrico bidimensional do canto, que está representado no detalhe (a), é delimitado pela diagonal de simetria adiabática e por uma seção da espessura da parede, na qual a distribuição de temperaturas é considerada ser linear entre e .
- Usando a rede nodal do detalhe (a), com L = 40 mm, determine a distribuição de temperaturas no elemento para e . Calcule a taxa de transferência de calor, para uma profundidade unitária (D = 1 m), se . Determine o fator de forma correspondente para o canto e compare o seu resultado com aquele da Tabela 4.1.
- Escolhendo um valor de n = 1 ou n = 1,5, estabeleça uma rede nodal para o trapézio mostrado no detalhe (b) e determine o campo de temperaturas correspondente. Avalie a validade da suposição da existência de distribuições lineares de temperaturas ao longo das seções a–a e b–b.
Passo 1
E por aqui a gente não para não !!
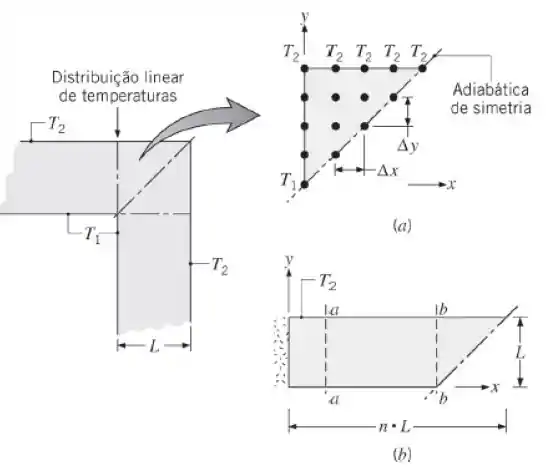
Na letra (a) nós vamos trabalhar com a figura (a) dada, vamos ver mais de perto?
Como a distribuição de temperatura é considerada linear entre e , nós vamos ter uma variação de 25°C a cada ponto, ok?
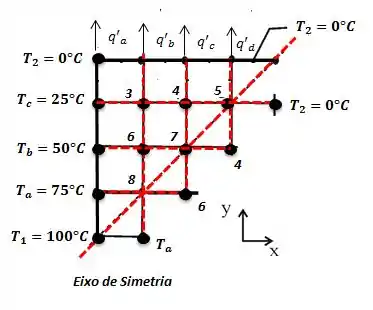
O que nós vemos aqui é que os pontos são nós internos, então a fórmula nestes casos é:
Fazendo para cada ponto:
Quando resolvemos as equações simultâneas com ajuda do nosso amado software:
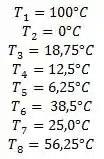
Já achamos a distribuição de temperaturas, agora nós precisamos da taxa de transferência de calor, ok?
Nós sabemos que:
E que a troca de calor com o ambiente vai se dar pela diferença de temperatura entre os pontos c, 3, 4 e 5 com relação a . Se é assim, para ambas as superfícies:
Substituindo:
Colocando nossos dados:
E ainda queremos o fator de forma, certo? Sabendo que:
E substituindo:
Quando olhamos na Tabela 4.1 nós vemos que o fator de forma vale 0,54, bem abaixo do que achamos, não foi?
Passo 2
Bom galera, na letra (b) nós vamos aumentar o espaçamento analisado onde temos a distribuição linear, ok?
A primeira que nós analisamos é mostrado pela letra (a), em seguida nós aumentamos uma coluna (b), e assim sucessivamente até (e).
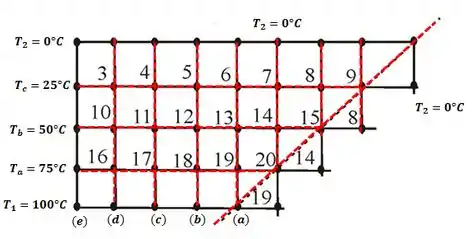
Quando nós fazemos o mesmo procedimento que do Passo 1 nós vamos obter os seguintes dados:
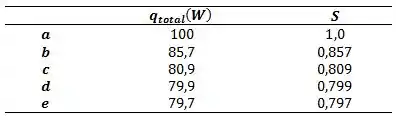
E finalizamos galerinha !!
Resposta