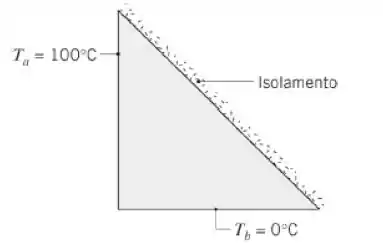
A diagonal de uma longa barra triangular se encontra isolada, enquanto as superfícies laterais, de comprimentos equivalentes, são mantidas a temperaturas uniformes Ta e Tb.
- Estabeleça uma rede nodal com cinco pontos nodais ao longo de cada um dos lados. Para um dos nós sobre a superfície diagonal, defina um volume de controle apropriado e deduza a equação de diferenças finitas correspondente. Usando essa expressão para os nós diagonais e equações apropriadas para os nós interiores, determine a distribuição de temperaturas na barra. Em um diagrama desenhado em escala, mostre as isotermas a 25, 50 e 75°C.
- Um procedimento alternativo e mais simples para obter as equações de diferenças finitas para os nós diagonais parte do reconhecimento de que essa superfície diagonal isolada é um plano de simetria. Considere uma rede nodal quadrada 5 × 5 e represente a sua diagonal como uma linha de simetria. Admita que os nós em cada um dos lados da diagonal tenham temperaturas idênticas. Mostre que você pode tratar os nós diagonais como nós “interiores” e escreva as equações de diferenças finitas por inspeção.
Passo 1
E por aqui a gente não para não !!
Na letra (a) nós vamos trabalhar com 5 nós por lados, isso nos dá:
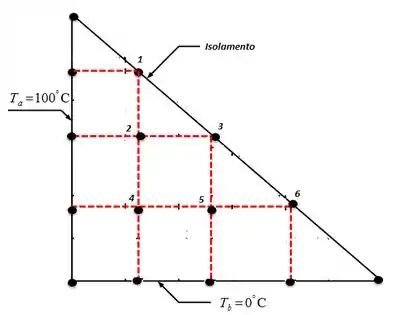
O que nós vemos aqui é que os pontos 2, 4 e 5 são nós internos, então a fórmula nestes casos é:
Fazendo para cada ponto:
Nós podemos fazer uma análise bem semelhante para os pontos na superfície adiabática, neste caso, como teremos apenas duas transferências de calor por condução, a fórmula ficará assim:
Aplicando nos pontos:
Quando resolvemos as equações simultâneas com ajuda do nosso amado software:

E as isotermas:
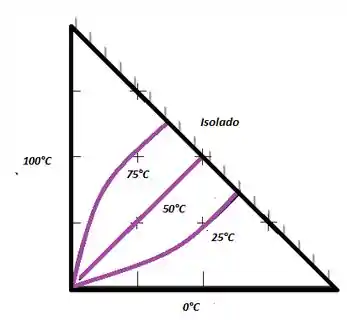
Já achamos a distribuição de temperaturas, agora nós precisamos da taxa de transferência de calor, ok?
Passo 2
Na letra (b) nós consideramos que, o que era isolado em (a) agora é um eixo simétrico!!
Se é um eixo de simetria nós podemos projetar os ponto da sua esquerda à direita, e o nosso desenho ficará assim:
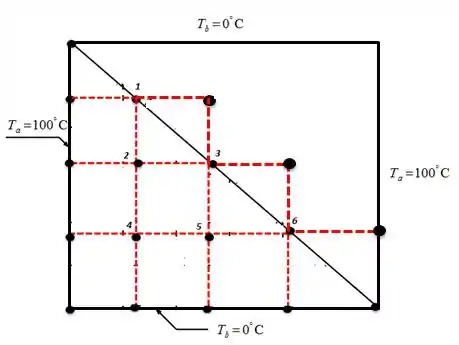
Então os nós 2, 4 e 5 continuam iguais:
Agora os nós nas diagonais serão interiores e, portanto:
Nooossa, olha que massaaa !!
Nós temos as mesmas equações, certo?
Por isso nós podemos concluir que neste caso a diagonal isolada pode ser tratada como um eixo de simetria!
E finalizamos galerinha !!