Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas para exames de fundamentos de engenharia - Ex. 4
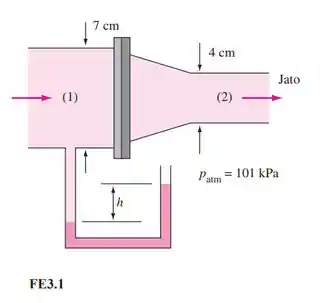
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se o fluido manométrico tem densidade de 1,6 e se , com o atrito desprezado, qual é a velocidade média na seção 2?
(a) 4,45 m/s, (b) 2,4 m/s, (c) 2,95 m/s, (d) 5,55 m/s, (e) 3,4 m/s.
Passo 1
O primeiro passo é encontrar a pressão em 1, para isto basta calcular a pressão hidrostática no manômetro:
Passo 2
Vamos encontrar uma relação entre e . Para isso é só utilizar a equação da continuidade:
Passo 3
Agora é só aplicar Bernoulli entre 1 e 2 e substituir as informações que temos. Vamos pegar os pontos na mesma altura para que e como a pressão em 1 já é a manométrica, vamos considerar :
Resposta
Letra C: (c) 2,95 m/s
Exercícios de Livros Relacionados
Dióxido de carbono escoa por um tubo isolado de 25 m de comprimento e 8 cm de diâmetro. O fator de atrito é 0,025. Na entrada, p = 300 kPa e T = 400 K. A vazão em massa é de 1,5 kg/s. Calcule a queda
Fazendo algumas substituições algébricas, mostre que a Equação (9.74) pode ser escrita na forma de massa específica ρ 1 2 = ρ 2 2 + ρ * 2 ( 2 k k + 1 * f L D + 2 l n ( ρ 1 / ρ 2 ) ) Por que essa fórmu
Ar escoa adiabaticamente em um duto de 3 cm de diâmetro. O fator de atrito médio é de 0,015. Se, na entrada, V = 950 m/s e T = 250 K, a que distância da entrada do tubo (a) o número de Mach será 1,8 o
Ar, fornecido a p 0 = 700 kPa e T 0 = 330K , escoa por um bocal convergente para dentro de um tubo de 2,5 cm de diâmetro que sai a uma condição de quase vácuo. Se fˉ ≈ 0,022, qual será a vazão em mass
O escoamento compressível com atrito em um duto, Seção 9.7, supõe entalpia de estagnação e vazão em massa constantes, porém quantidade de movimento variável. Tal escoamento normalmente se denomina esc