Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 36

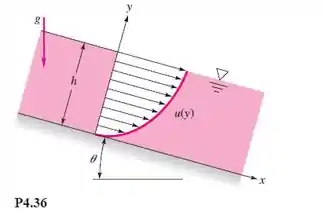
Um filme de espessura constante de um líquido viscoso flui em movimento laminar descendo por uma placa inclinada a um ângulo θ , como na Figura P4.36. O perfil de velocidade é

u = C y 2 h - y                 v = w = 0

Encontre a constante C em termos do peso específico e da viscosidade e do ângulo θ . Encontre a vazão volumétrica Q por unidade de largura em termos desses parâmetros.

Passo 1

Simbora lá pra mais uma!

Existe uma pressão atmosférica ao longo de todo o corpo em y = h , portanto, teremos ∂ p ∂ x = 0 . Podemos fazer facilmente a equação de momento em x, temos o perfil de velocidade ainda, bora lá!

ρ u ∂ u ∂ x + v ∂ v ∂ y = - ∂ p ∂ x + ρ g x + μ ∇ 2 u

Substituindo os perfis e utilizando uma relação trigonométrica para g, teremos:

0 = 0 + ρ g sen ⁡ θ + μ ( - 2 C )

C = ρ g sen ⁡ θ 2 μ

Passo 2

Okay, encontramos (a) já! Bora pra (b).

A vazão volumétrica por unidade de largura é encontrada integrando nosso perfil de velocidade e usando o C que encontramos, assim:

Q = ∫ 0 h u d y = ∫ 0 h C y 2 h - y d y = 2 3 C h 3 = ρ g h 3 sen ⁡ θ 3 μ

Resposta

C = ρ g sen ⁡ θ 2 μ

Q = ρ g h 3 sen ⁡ θ 3 μ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Compare o fator de forma H (definido na Equação 10-95) para uma camada limite laminar versus camada limite turbulenta sobre uma placa plana, assumindo que a camada limite turbulenta é turbulenta desde
Para a aproximação linear do Problema 10 - 83 , use a definição de coeficiente local de atrito superficial e a equação integral de Kárman para gera uma expressão para δ / x . Compare o seu resultado c
Calcule o valor do fator de forma H para o caso limite de uma camada limite que é infinitesimalmente fina (Figura P 10 - 89 ). Esse valor de H é o valor mínimo possível.
O perfil de Blasius da camada limite é uma solução exata das equações da camada limite para escoamento sobre uma placa plana. No entanto, os resultados são um pouco incômodos de usar, pois os dados ap
Para a aproximação da onda senoidal do Problema 10 - 85 , use a definição de coeficiente local de atrito superficial e a equação integral de Kárman para gerar uma expressão para δ / x . Compare o seu