Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 15
Um fluido incompressível e invíscido escoa para dentro de um tubo circular, horizontal, através de sua parede porosa. O tubo é fechado na extremidade esquerda e o escoamento descarrega para a atmosfera pela extremidade direita. Para simplificar, considere a componente x da velocidade uniforme através de qualquer seção transversal no interior do tubo. A massa específica do fluido é ρ, o diâmetro e o comprimento do tubo são D e L, respectivamente, e a velocidade uniforme de entrada do fluido é . O escoamento é em regime permanente. Obtenha uma expressão algébrica para a componente x da aceleração de uma partícula fluida localizada na posição x, em termos de , x e D. Encontre uma expressão para o gradiente de pressão, ∂p/∂x, na posição x. Integre para obter uma expressão para a pressão manométrica em x = 0.
Passo 1
Pessoal, este é um problema de escoamento unidirecional que pede a aceleração e gradiente de pressão. Para começar, vamos aplicar a equação da aceleração 5.11a:
Assumindo que:
- regime permanente
- fluido incompressível
- fluxo uniforme pela seção
- Velocidades de escoamento em y e em z são nulas.
A equação simplifica para:
Passo 2
Agora vamos aplicar a conservação de massa para um volume de controle no contorno de r:
Com as considerações do passo anterior, a equação simplifica para:
Agora devemos ver pelo desenho o que isto significa.
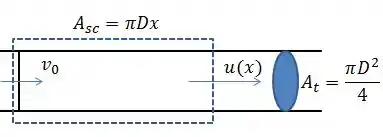
O que está saindo do tubo equivale a:
Já o que está dentro do tubo, vale (ver demonstração no exercício 4.123):
Então ficamos com a equação:
Agora basta substituir na equação da aceleração:
Passo 3
Para encontrar o gradiente de pressão vamos usar a equação de Euler 6.2a do livro:
Pela equação da aceleração do Passo 1, podemos simplificar a expressão acima:
Substituindo o valor de
Como o fluxo é apenas em x, podemos usar a relação:
Substituindo e integrando:
Como