Quando o fluido que sai por um bocal, como na Figura P3.49, for um gás em vez de água, a compressibilidade pode ser importante, especialmente se a pressão a montante p1 for alta e o diâmetro de saída d2 for pequeno. Neste caso, a diferença p1 - p2 não controla mais o fluxo e a vazão em massa do gás m alcança um valor máximo que depende de p1 e d2 e também da temperatura absoluta a montante T1 e da constante R do gás. Assim, funcionalmente, m= f(p1, d2, T1, R). (a) Usando análise dimensional, reescreva essa função em forma adimensional.(b) Um certo tubo tem d2 = 1 mm. Para escoamento de ar, as medidas mostram os seguintes valores de vazão em massa através do bocal:

Faça um gráfico desses dados na forma adimensional obtida na parte (a). O seu gráfico revela a relação funcional completa obtida na parte (a)?

Em primeiro lugar, iremos resolver a letra (a).

Vamos olhar de novo a função que define a vazão mássica do gás:

Note que nessa função temos variáveis e dimensões primárias (). Por análise dimensional, sabemos que isso quer dizer que teremos apenas 1 grupo Pi, que será:

Pra finalizar a questão, vamo resolver a letra (b).

Nesse passo, iremos plotar um gráfico de em função da temperatura do gás

Lembre que temos um diâmetro e que, para o ar, .

Desta forma, podemos calcular as velocidades com base nos valores de vazão mássica , temperaura e pressão apresentados na Tabela que ilustra o problema.

A tabela abaixo demonstra os resultados cálculos que fizemos para cada conjunto de valores , , :

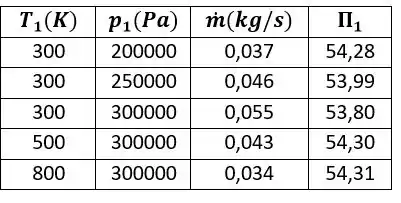
O enunciado nos fala pra traçar um gráfico, mas podemos perceber que o valor de é, na prática, uma constante cujo valor parece ser aproximadamente .

Pronto, matamos a questão juntos!