Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 24
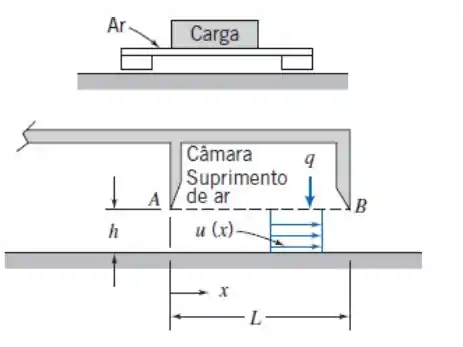
Grandes cargas podem ser movimentadas com relativa facilidade sobre colchões de ar com o emprego de uma plataforma de carga, conforme mostrado. O ar é suprido da câmara (ou pleno) através da superfície porosa AB. Ele penetra no espaço abaixo da plataforma verticalmente com velocidade uniforme, q. Neste espaço, todo o ar escoa no sentido positivo do x (não há escoamento através do plano em x = 0). Considere que o fluxo de ar na fresta é incompressível e uniforme em cada seção, com velocidade u(x), conforme mostrado na vista ampliada. Embora a fresta seja estreita (h ≪ L), despreze efeitos de atrito em primeira aproximação. Use um volume de controle adequadamente escolhido para mostrar que u(x) = qx/h na fresta. Calcule a aceleração de uma partícula fluida na fresta. Avalie o gradiente de pressão, ∂p/∂x, e esboce a distribuição de pressão através da fresta. Certifique-se de indicar a pressão em x = L.
Passo 1
Pessoal, vamos primeiro provar que. Para isto iremos aplicar a equação da conservação de massa:
Como o liquido esta sendo espremido e saindo pelas laterais, haverá variação de massa no sistema. Uma vez que as placas são planas e considerando uma variação infinitesimal na altura, a equação será reduzida para:
Podemos observar pela figura que a variação de altura pela placa superior em função do tempo é –q.
Substituindo:
Passo 2
A equação da aceleração da partícula em x é dada pela equação:
Considerando:
-fluido incompressível;
-regime permanente;
-fluxo constante por toda a seção;
-fluxo horizontal e;
-velocidade nula em z.
Podemos simplificar a expressão e ficamos com:
Passo 3
Para encontrar o gradiente de pressão, vamos usar a equação de Euler em x:
Substituindo e sendo :
Passo 4
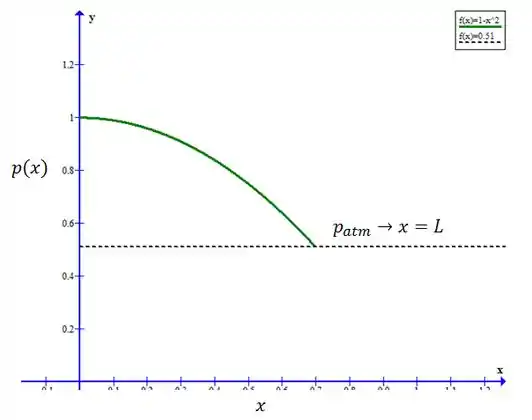
A distribuição de pressão pode ser encontrada integrando a equação do gradiente:
Substituindo e integrando a equação, temos:
Esboçando o gráfico, temos:
