Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 128
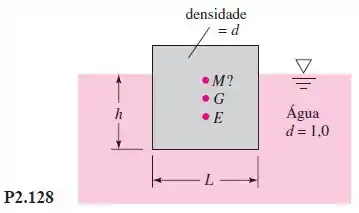
Um iceberg pode ser idealizado como um cubo de lado , como na Figura P2.128. Se a água do mar for representada por , então o gelo da geleira (que forma os icebergs) tem . Determine se esse iceberg “cúbico” é estável para a posição mostrada na Figura P2.128.
Passo 1
Fala galera, vem comigo resolver essa questão!!
Queremos aqui determinar se esse iceberg “cúbico” é estável para a posição mostrada. Para isso, podemos começar usando a ideia de que as forças que atuam verticalmente o mantém em equilíbrio, ou seja, a soma das forças é igual a zero. Assim temos:
Aqui, é o volume de líquido deslocado, é o volume do iceberg, é o peso especifico da água do mar e é o peso especifico do iceberg.
Podemos substituir como foi dito no enunciado.
Não vamos substituir pois vamos verificar a estabilidade a partir dele.
Passo 2
Para encontrarmos o que estamos procurando, podemos usar a formula 2.37:
Em que é o centróide, é o metacentro, é o centro de flutuabilidade, é o momento de inércia e é o volume submerso. Para um cubo o momento de inercia é dado por:
O volume submerso para essa questão é:
Para a estabilidade de massa precisamos que:
O centro de gravidade está em acima do fundo e está em acima do fundo. Para essa questão a distancia é dada por:
Passo 3
Agora que temos todos os dados, vamos substituir na equação 2.37.
O iceberg “cúbico” só será estável se , então vamos impor . Assim temos:
Se usarmos a formula de Bhaskara, vamos encontrar que
Passo 4
Agora, podemos plotar um gráfico para melhor visualizar.
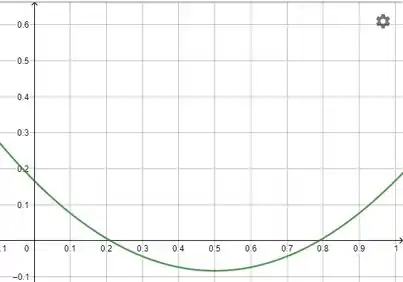
Podemos perceber que ele é estável quando
Foi dito no enunciado que
Portanto o iceberg é estável pois está no valor estipulado pelo cálculo.
Resposta
É estável pois