Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 4.Problemas - Ex. 72

Uma longa barra com seção transversal retangular, de 60   m m × 90   m m , tem condutividade térmica igual a 1   W / m · K . Uma superfície está exposta a um processo de convecção com ar a 100°C e um coeficiente convectivo de 100   W / m 2 · K , enquanto as superfícies restantes são mantidas a 50 ° C .

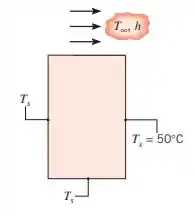
(a) Usando uma malha com espaçamento de 30   m m e o método iterativo de Gauss-seidel, determine as temperaturas nodais e a taxa de transferência de calor do ar para a barra, por unidade de comprimento normal à página.

Passo 1

Bora resolver essa questão comigo?

Vamos lá!

Começamos com o espaçamento da grade ∆ x = ∆ y = 30     m , três nós somos criados.

Utilizando as equações de diferenças finitas conforme mostrado na Tabela 4.2, mas escritas na forma exigida pelo método de Gauss-Seidel (Apêndice D), e com:

B i = h ∆ x k = 100 ⋅ 0,030 1 = 3

Temos assim:

- Nó 1:

T 1 = 1 B i + 2 T 2 + T s + B i T ∞ = 1 5 T 2 + 50 + 3 × 100 = 1 5 T 2 + 350

- Nó 2:

T 2 = 1 4 T 1 + 2 T s + T 3 = 1 4 T 1 + T 3 + 2 ⋅ 50 = 1 4 T 1 + T 3 + 100

- Nó 3:

T 3 = 1 4 T 2 + 3 T s = 1 4 T 2 + 3 ⋅ 50 = 1 4 T 2 + 150

Passo 2

Realizando uma série de iterações para obtermos as nossas temperaturas, começando com o chute inicial ( k = 0 ) :

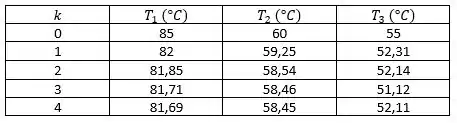
Na quarta interação, percebemos que as mudanças são muito pequenas em relação a sua anterior, sugerindo assim que cálculos adicionais podem não ser necessários.

Passo 3

Calculando a taxa de transferência de calor do ar para a barra:

q c o n v ' = h ∆ x 2 T ∞ - T s + h ∆ x T ∞ - T 1 + h ∆ x 2 T ∞ - T s

q c o n v ' = h ∆ x T ∞ - T s + h ∆ x T ∞ - T 1

q c o n v ' = h ∆ x T ∞ - T s + T ∞ - T 1

Substituindo os dados:

q c o n v ' = 100 ⋅ 0,030 ⋅ 100 - 50 - 100 - 81,7

q c o n v ' = 205   W / m

Até a próxima questão!

Resposta

q c o n v ' = 205   W / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bastão de sustentação ( k = 15W / ( m · K ) , α = 4,0 × 10 - 6m 2 / s ), com diâmetro D = 15m m e comprimento L = 100m m , atravessa um canal cujas paredes são mantidas a uma temperatura de T b = 3
Considere o sistema do Problema 4.92. Inicialmente, sem o escoamento dos gases de exaustão, as paredes ( α=5,5×10 - 7m 2 / s ) se encontram a uma temperatura uniforme de 25 ° C . Usando o método implí
Seja o elemento combustível do Exemplo 5.11, que opera a uma taxa volumétrica de geração uniforme de 1 = 107 W/m3, até que a taxa de geração mude subitamente para 2 = 2 × 107 W/m3. Use o software de e
Considere o sistema do Problema 4.86. Inicialmente, a placa cerâmica ( α = 1,5×10 - 6m 2 / s ) se encontra a uma temperatura uniforme de 30 ° C . Subitamente, os elementos elétricos de aquecimento são
Duas barras muito longas (na direção normal à página) com as distribuições iniciais de temperaturas mostradas na tabela, devem ser soldadas lateralmente uma à outra. No tempo t=0 , a face equivalente