Um tanque esférico de de diâmetro contém um gás de petróleo liquefeito a . Isolamento com condutividade térmica de e espessura de é aplicado ao tanque para reduzir o ganho de calor.

(a) Determine a posição radial na camada de isolamento em que a temperatura é quando a temperatura do ar ambiente é e o coeficiente de convecção na superfície externa é .

(b) Se o isolamento é permeável à umidade do ar atmosférico, a que conclusões você pode chegar sobre a formação de gelo no isolamento? Que efeito a formação de gelo terá no ganho de calor para o gás LP? Como essa situação pode ser evitada?

Os dados fornecidos foram:

Diâmetro do tanque:

Raio do taque:

Espessura do isolamento:

Raio:

Condutividade térmica do isolamento:

Coeficiente de convecção na superfície externa:

Temperatura na superfície interna:

Temperatura do ambiente:

Temperatura no isolamento em:

(a) Para resolver essa questão, podemos fazer um circuito térmico que representa a condução de calor no sistema. O circuito tem a seguinte forma:

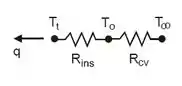
Do circuito térmico, temos que o ganho de calor para o tanque é dado por:

onde as resistências térmicas para o isolamento e o processo de convecção na superfície externa são, respectivamente

Logo, temos que o ganho de calor é:

Nós consideramos que a condução de calor é constante e que não existe perda, portanto, podemos dizer que

Portanto:

Substituindo os termos da expressão acima pelos dados fornecidos, temos:

Portanto, o raio em que a temperatura é é .

(b) Para entender o que está acontecendo, é bom lembramos que em , a temperatura é , ou seja, a partir desse ponto pode ocorrer a formação de gelo se o isolamento for permeável ao vapor de água. O efeito da formação de gelo é aumentar substancialmente o ganho de calor, uma vez que é quase duas vezes maior que , e a região de gelo é de espessura . Para evitar a formação de gelo, uma barreira de vapor deve ser instalada em um raio maior que .