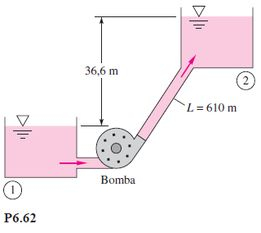
PA11.8 – Uma bomba-turbina é um dispositivo reversível que usa um reservatório para gerar energia durante o dia e depois bombeia a água de volta para o reservatório durante a noite. Vamos redefinir o Problema P6.62 como uma bomba-turbina. Recorde-se que Δz=36,6 m e que a água escoa através de 610 m de tubo de ferro fundido de 152 mm de diâmetro. Para simplificar, suponha que a bomba opera no PMR (92%) com H*Bomba=61 m e que a turbina opera no PMR (89%) com H*Turbina=30,5 m. Despreze as perdas localizadas. Calcule (a) a potência de eixo, em watts, necessária para a bomba; e (b) a potência, em watts, gerada pela turbina. Para outras leituras técnicas, consulte o URL www.usbr.gov/pmts/hydraulics_lab/pubs/EM/EM39.pdf.

Vamos agora revisar Ph

Ph como foi dito, é a potência hidráulica, e esta representa a quantidade total de energia que a bomba transmitiu para o fluido.

Essa variável, lembrando então, é função das propriedades do fluido e da vazão do fluido. A expressão para ela é a seguinte

Onde,

-ρ é a massa especifica (densidade) do fluido (água), que vale 998kg/m3 para a água;

-g é constante da gravidade, g=9,81 m/s2;

-Q é a vazão do fluido;

-HBomba é a altura de carga da bomba;

Substituindo, a expressão para a eficiência da bomba agora é

Isolando Pe,Bomba

Precisamos da vazão, Q

Podemos achar a vazão pela velocidade de escoamento do fluido, que podemos achar pela equação de Darcy-Weisbach da perda de carga

Onde,

hLT é a perda de carga total do sistema, devido ao atrito do fluido com a tubulação e ao atrito com os acessórios localizados;

-hac é a perda de carga localizada;

-hp é a perda de carga por atrito na tubulação;

-f é o fator de atrito;

-LT é o comprimento total da tubulação;

-DT é o diâmetro interno da tubulação;

-V é a velocidade do fluido na tubulação;

-Ki é uma constante que é especifica para cada tipo de acessório localizado na tubulação;

-g é a constante da gravidade, g=9,81 m/2.

Foi dito para desprezarmos as perdas localizadas, então

Para expressarmos em termos de vazão, podemos usar a seguinte relação entre vazão e velocidade de escoamento

Onde,

-Q é a vazão volumétrica;

-A é a área da seção transversal do tubo;

-V é a velocidade do fluido.

A área de seção transversal é função do diâmetro da tubulação

Assim,

Isolando V

Substituindo na Eq3

Fazendo um balanço de energia mecânica (Eq. de Bernoulli), conseguimos determinar quem é hp.

Relembrando da equação de Bernoulli aplicada para processos com máquinas de fluxo é

Onde,

- HBomba é a altura de carga da bomba, que é a energia que a bomba deve fornecer ao fluido;

-Δp é a variação de pressão do sistema;

-ΔV2 é a variação de energia cinética do sistema;

-Δz é a variação de energia potencial do sistema;

-hLT é a perda de carga total do sistema, devido ao atrito do fluido com a tubulação e ao atrito com os acessórios;

-ρ é a densidade do fluido;

-g é a constante da gravidade, g=9,81 m/s2.

Para hLT

Onde,

-hp e hac são a perda de carga devido ao atrito do fluido com a tubulação e a perda de carga devido ao atrito com os acessórios, respectivamente;

Aplicando o balanço de energia mecânica (Eq de Bernoulli) entre o reservatório de baixo (1) e o reservatório de cima (2), da figura P6.62, lá em cima no enunciado

Onde,

-p1 e p2 são a pressão no reservatório de baixo e no de cima, respectivamente;

-V1 e V2 são a velocidade do fluido no reservatório de baixo e no de cima, respectivamente;

-z1 e z2 são a altura no nível no reservatório de baixo e no de cima, respectivamente;

-hp é a perda de carga por atrito do fluido na tubulação;

-ρ é a densidade da água, ρ=998 kg/m3;

-g é a constante da gravidade, g=9,81 m/s2.

Na Eq5 não foi adicionado o termo hac, pois foi pedido para desprezar as perdas localizadas.

Isolando HBomba

Vamos agora analisar a figura P6.62, lá em cima para ver quem é quem da equação de Bernoulli.

Analisando o esquema da figura P6.62, vemos que

Onde, patm é a pressão atmosférica que você pode considerar para as duas pressões, pois os dois reservatórios estão abertos para a atmosfera.

Também vemos que as velocidades em 1 e 2 são referentes as velocidades de nível de fluido nos reservatórios, e como estes são de grande dimensão (D muito alto), então as velocidades são muito pequenas. Assim,

Já para as alturas z1 e z2, temos pela figura que

A Eq. da altura de carga da bomba, HBomba agora é

Isolando hp

Calculando

Voltando na Eq4

Isolando Q

Para encontrarmos Q, precisaremos de f, o fator de atrito

O fator de atrito depende de Reynolds (Re) e da rugosidade relativa, ε/D

Pelo problema 6.62, o tubo é de ferro fundido e para este material a rugosidade, ε, vale

A equação de Reynolds é

Onde,

-Re é o número de Reynolds;

-ρ é a densidade do fluido (água), ρ=998 kg/m3 para a água;

-DT é o diâmetro da tubulação, pelo problema 6.62, DT=152mm=0,152m;

-Q é a vazão do fluido;

-μ é a viscosidade dinâmica do fluido (água), μ=0,001 kg/m.s para a água;

Calculando Re:

Você pode ver que Re precisa de Q, mas não temos Q, que é o que queremos achar. Então, Re depende de Q, f depende de Re e Q depende de f, não podemos dessa forma determinar diretamente o valor de nenhum nem outro. O que temos que fazer é usar um método iterativo para encontrar a solução desse problema. Lembrando que um método iterativo você precisa dar um chute inicial para alguma das variáveis e a partir desse chute inicial você começa a calcular com as equações, pegando os valores calculados e atualizando o chute e recalculando novamente até que seja atingido uma convergência. Essa convergência você pode verificar da seguinte maneira: pegue o valor anterior calculado e diminua pelo novo valor calculado, estipule uma tolerância, ai quando essa diferença for menor que a tolerância você chegou em uma convergência.

• Algoritmo Resolução pelo método iterativo:

I – chute inicial para f (você pode olhar no diagrama de Moody a faixa de valores de f);

II – calcula Q pela equação

III – calcula Re pela equação

IV – determina novo valor de f usando diagrama de Moody ou a Eq. de Churchill

V – calcula novo valor de Q pela mesma equação;

VI – calcular a diferença percentual (erro) entre o novo valor de Q com o valor anterior pela expressão

VII – verificar se erro é menor que a tolerância (estipular um valor da tolerância, um valor muito pequeno, tipo uns 10-5%);

VIII – se o erro for maior que a tolerância, você volta a etapa III para uma nova iteração; (você vai continuar as iterações até que o erro seja menor que a tolerância)

Se você fizer este método iterativo à mão, vai levar algum trabalho. A melhor opção é usar um programa computacional, como o MATLAB, ou Python, ou até mesmo o EXCEL.

Para resolver eu usei o EXCEL, este é o mais simples. Abaixo o print do método no EXCEL.

Veja pela imagem acima que na iteração de nº 5 já temos um erro percentual de 0,000078%, e também veja que o valor de Q, praticamente não se altera mais a partir dessa iteração. Portanto, houve uma convergência na iteração 2.

Os valores convergidos foram:

Agora que temos a vazão, podemos calcular a potência requerida pela bomba pela Eq1

Substituindo os valores

B)

Analogamente para a turbina, você vai fazer literalmente os mesmos passo a passo, como feito para a bomba.

O que terá de diferente é o cálculo da potência de eixo gerada pela turbina, Pe,Turbina

Calculando Pe,Turbina pela expressão de rendimento da turbina.

O rendimento da turbina é a quantidade de potência que o equipamento gerou, Pe, dividido pela quantidade de potência disponível que a turbina tem para receber do fluido, PH, cuja expressão é

Onde,

-ηturbina é o rendimento da turbina;

-Pe é a potência de eixo de saída da turbina;

-PH é a potência hidráulica disponível, é a potência que a turbina recebe do fluido;

O rendimento da turbina pode ser entendido também da seguinte forma: é a quantidade percentual de energia que a turbina recebeu do fluido, ou melhor, a quantidade percentual de energia que a turbina removeu do fluido, que escoa por dentro da turbina, para gerar a potência de eixo.

Revisando PH

PH como foi dito, é a potência hidráulica disponível, e esta representa a quantidade total de energia disponível que o fluido possui para fornecer à turbina.

Essa variável, lembrando então, é função das propriedades do fluido e da vazão do fluido. A expressão para ela é a seguinte

Onde,

-ρ é a massa especifica (densidade) do fluido;

-g é constante da gravidade, g=9,81 m/s2;

-Q é a vazão do fluido;

-HTurbina é a altura de queda da turbina, a energia que a turbina remove do fluido;

Substituindo, a expressão para a eficiência agora é

Isolando Pe

Agora é o mesmo processo do que foi feito na questão A) para determinar Q

Então, analogamente

Pela Eq. de Bernoulli

Veja que na equação de Bernoulli para a bomba chegamos na expressão

Para a turbina o termo de hp está com sinal negativo, isso porque a turbina remove energia do fluido para gerar potência de eixo, então essa perda de carga (hp) , isto é, perda de energia do fluido é uma energia não é aproveitada pela turbina. E no caso da bomba, o sinal fica positivo, pois é uma energia que a bomba deve fornecer ao fluido para suprir a perda de carga, a perda de energia que o fluido sofreu.

Continuando, então. Isolando hp

Calculando

Pela Eq. de Darcy-Weisbach

Vamos isolar Q e chegar em

O fator de atrito é por Reynolds e rugosidade

Agora vamos para as iterações, também de forma análoga da parte (A)

Algoritmo Resolução pelo método iterativo:

I – chute inicial para f (você pode olhar no diagrama de Moody a faixa de valores de f);

II – calcula Q pela equação

III – calcula Re pela equação

IV – determina novo valor de f usando diagrama de Moody ou a Eq. de Churchill

V – calcula novo valor de Q pela mesma equação;

VI – calcular a diferença percentual (erro) entre o novo valor de Q com o valor anterior pela expressão

VII – verificar se erro é menor que a tolerância (estipular um valor da tolerância, um valor muito pequeno, tipo uns 10-5%);

VIII – se o erro for maior que a tolerância, você volta a etapa III para uma nova iteração; (você vai continuar as iterações até que o erro seja menor que a tolerância)

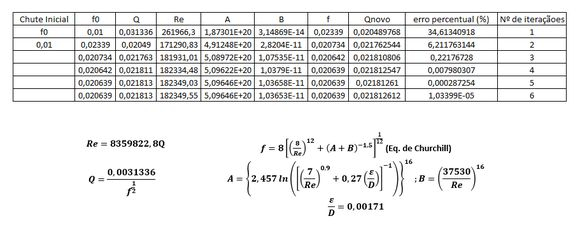
Pela imagem acima

Agora que temos a vazão, podemos calcular a potência requerida pela bomba pela Eq1

Substituindo os valores