Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 53

Uma longa barra condutora com seção transversal retangular ( 20   m m   ×   30   m m ) e condutividade térmica k   =   20 W m K , experimenta geração térmica uniforme a uma taxa de q ˙ =   5   ×   10 7 W m 3 , enquanto suas superfícies são mantidas a 300 K.

  1. Usando o método de diferenças finitas com um espaçamento na malha de 5 mm, determine a distribuição de temperaturas na barra.
  2. Mantidas as mesmas condições de contorno, qual taxa de geração de calor irá causar uma temperatura de 600 K no ponto central da barra?

Passo 1

Vamnos pra mais uma??

Aqui nós precisamos desenhar para conseguir ver melhor o que vai rolar !!

Nós vamos dividir a direção x em 6 espaçamentos, enquanto a direção y nós dividimos em 4 para que eles fiquem iguais entre si!!

Nós temos que pensar na simetria dentro do retângulo certo, e aí conseguimos chegar ao desenho:

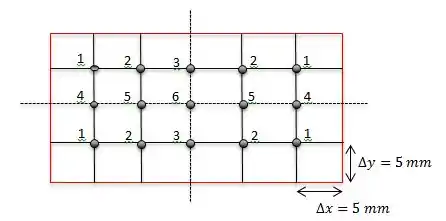
Como todos os nós são interiores nós podemos usar a seguinte equação:

T i = 1 4 ∑ T v i z i n h o s + 1 4 q ˙ ∆ x ∆ y k

Como ∆ x = ∆ y :

T i = 1 4 ∑ T v i z i n h o s + 1 4 q ˙ ∆ x 2 k = 1 4 ∑ T v i z i n h o s + 15,625

Achando cada uma separadamente:

T 1 = 1 4 T s + T s + T 2 + T 4 + 15,625 = 0,25 600   K + T 2 + T 4 + 15,625

T 2 = 1 4 T s + T 1 + T 3 + T 5 + 15,625 = 0,25 300   K + T 1 + T 3 + T 5 + 15,625

T 3 = 1 4 T s + T 2 + T 6 + T 2 + 15,625 = 0,25 300   K + 2 T 2 + T 6 + 15,625

T 4 = 1 4 T s + T 1 + T 5 + T 1 + 15,625 = 0,25 300   K + 2 T 1 + T 5 + 15,625

T 5 = 1 4 T 2 + T 6 + T 2 + T 4 + 15,625 = 0,25 2 T 2 + T 4 + T 6 + 15,625

T 6 = 1 4 T 3 + T 5 + T 3 + T 5 + 15,625 = 0,25 2 T 3 + 2 T 5 + 15,625

Para resolver estas equações nós podemos usar o solver do Excel ou em outro software que vocês prefiram, ok?

T 1 = 348,6   K

T 2 = 368,9   K

T 3 = 374,6   K

T 4 = 362,4   K

T 5 = 390,2   K

T 6 = 398,0   K

Passo 2

Bom galerinha, na letra (b) nós temos que achar o valor do calor q ˙ sabendo que T 6 = 600   K , então:

T i = 1 4 ∑ T v i z i n h o s + 1 4 q ˙ ∆ x 2 k

T i = 0,25 ∑ T v i z i n h o s + q ˙ 3,125 × 10 - 7

Então nossas equações vão ficar assim:

T 1 = 0,25 600   K + T 2 + T 4 + q ˙ 3,125 × 10 - 7

T 2 = 0,25 300   K + T 1 + T 3 + T 5 + q ˙ 3,125 × 10 - 7

T 3 = 0,25 900   K + 2 T 2 + q ˙ 3,125 × 10 - 7

T 4 = 0,25 300   K + 2 T 1 + T 5 + q ˙ 3,125 × 10 - 7

T 5 = 0,25 2 T 2 + T 4 + 600   K + q ˙ 3,125 × 10 - 7

600   K = 0,25 2 T 3 + 2 T 5 + q ˙ 3,125 × 10 - 7

Resolvendo novamente nossas equações vamos obter:

q ˙ = 1,53 × 10 8 W m 3  

Tranquilinha, não é?

Resposta

  1. T 1 = 348,6   K   |   T 2 = 368,9   K   |   T 3 = 374,6   K   |   T 4 = 362,4   K   |   T 5 = 390,2   K   |   T 6 = 398,0   K ;
  2. q ˙ = 1,53 × 10 8 W m 3 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 4 00m m de lado. As paredes são construídas com tijolos refratários com 20 0m m de espessura e condutivid
Considere uma aleta plana triangular, bidimensional, com comprimento L = 50m m e espessura na base de t = 20m m . A condutividade térmica da aleta é k = 25W / m · K . A temperatura de sua base é T b =
47 – Canais quadrados de dimensão LC = 20,5(10 mm) = 14,14 mm são uniformemente espaçados em S=25 mm ao longo da linha central de um prato de espessura Lp= 40 mm. Fluido frio e quente escoam através d
113 – Uma chaminé passando gases quentes de exaustão tem uma área de seção transversal quadrada de 300 mm de lado. As paredes são construídas de tijolos refratários de 150 mm de espessura com uma cond
114 – Elementos de aquecimento elétrico de pequeno diâmetro dissipando 50W/m são usados para aquecer um prato de cerâmica de condutividade térmica 2W/m.K. A superfície de cima do prato está exposta ao