Plantadores usam ventiladores gigantescos para evitar o congelamento de uvas quando a temperatura efetiva do céu é baixa. A uva, que pode ser vista como uma fina película, com resistência térmica desprezível que encerra um volume de água açucarada, está exposta ao ar ambiente e é irradiada pelo céu e pelo solo. Considere a uva uma esfera isotérmica com de diâmetro e admita irradiação de corpo negro uniforme sobre os seus hemisférios superior e inferior devido às emissões do céu e da Terra, respectivamente.

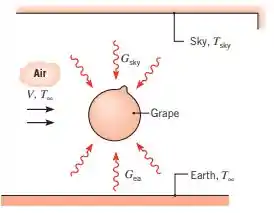
(a) Deduza uma expressão para a taxa de variação da temperatura da uva. Expresse seu resultado em termos de um coeficiente convectivo e de temperaturas e grandezas radiantes apropriadas.

(b) Sob condições nas quais , e o ventilador desligado , determine se as uvas irão congelar. Com uma boa aproximação, a emissividade da película é igual a 1 e as propriedades termo físicas da uva são aquelas da água sem açúcar. Entretanto, devido à presença do açúcar, as uvas congelam a .

(c) Com todas as demais condições permanecendo sem alteração, com exceção do fato de que agora os ventiladores estão operando e proporcionando uma , as uvas irão congelar?

Letra a)

Aplicando um balanço de energia na superfície de controle sobre a uva:

Sendo:

Temos que a taxa de variação da temperatura com o tempo é:

Letra b)

Aqui, devemos conferir se as uvas irão congelar.

Calculando o número de Rayleigh:

Calculando o número de Nusselt:

Calculando :

Assim, a taxa de variação da temperatura com o tempo é:

Como:

Letra c)

Para .

Calculando o número de Reynolds:

Com:

Calculando o número de Nusselt:

Assim, a taxa de variação da temperatura com o tempo é:

Como:

E como possuímos um valor maior do que o encontrado na letra (b), a uva congelará mais cedo.