Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 39

Repita o Problema 10-38, mas supondo que o fluido em rotação é óleo de motor a 60°C. Discuta.

Passo 1

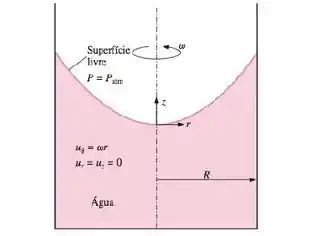
Turubem? Esse aí é nosso desenhozinho da questão anterior que a gente tava usando água.

Vamos começar pela componente r da equação de Euler:

- ρ u θ 2 r = - ∂ P ∂ r → ∂ P ∂ r = ρ w 2 r

Componente z:

- ∂ P ∂ z = ρ g → ∂ P ∂ z = - ρ g  

Agora a gente vai integrar nossa equação da componente r e vamos ter:

P = ρ w 2 r 2 2 + f ( z )

Aí você tá me perguntando assim: WTF QUE É ESSA f(z)! Calma, meu amigo, te explicar... A gente acrescentou uma função de z porque estamos partindo de uma integral PARCIAL. Olha porque eu fiz isso:

  1. Primeiro pega a equação acima e deriva em função de z
  2. A gente tem pela equação da componente em z quem é a derivada da pressão em função de z
  3. Igualamos e sejamos felizes depois com uma integração chupetinha rs

∂ P ∂ z = f ' z = - ρ g → f z = - ρ g z + C 1

Tchururu!!! Vamos agora pegar a equação que representa a função de z e jogar na nossa equação anterior, ok?

P = ρ w 2 r 2 2 - ρ g z + C 1

Passo 2

Agora fica mais tranquilo!!!!

Bem, a gente sabe que em r=0 e z=0 vamos ter P=Patm = C1

Por fim olha que lindeza:

O campo de pressão pode ser dado por P = ρ w 2 r 2 2 - ρ g z + P a t m

E para forma de superfície: Z s u p e r f = w 2 r 2 2 g

Note que aqui as equações são as MESMAS do problema anterior, a única diferença está no valor da densidade. Com isso concluímos que a densidade do fluido NÃO afeta a forma de superfície e também a equação do campo de pressão!

Resposta

P = ρ w 2 r 2 2 - ρ g z + P a t m

Z s u p e r f = w 2 r 2 2 g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.2 Um campo de escoamento incompressível e sem atrito é dado por V → = A x + B y i ^ + B x - A y j ^ , em que A = 2 s - 1 , B = 2 s - 1 e as coordenadas são medidas em metros. Determine o módulo e o
6.7 Considere o campo de escoamento dado por V → = A xs e n2 π ω t i ^ + A ys e n2 π ω t j ^ , em que A = 2s - 1 e ω = 1s - 1 . A massa específica do fluido é 2 kg/m³. Encontre expressões para a acele
Em um escoamento bidimensional sem atrito e incompressível (ρ = 1500 kg/m3), o campo de velocidade em m/s é dado por V → = A x + B y i ^ + B x - A y j ^ , as coordenadas são medidas em metros, e A = 4
O campo de velocidade para um dipolo plano é dado na Tabela 6.2. Determine uma expressão para o gradiente de pressão em qualquer ponto ( r ,θ ).
Um “chip” retangular de microcircuito flutua sobre uma fina camada de ar, com espessura h = 0,5 mm, acima de uma superfície porosa. A largura do chip é b = 40 mm, conforme mostrado. O seu comprimento,