Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 124

Determine a distribuição de temperaturas em t   =   30   m i n para as condições do Problema 5.116 .

(a) Use uma técnica de diferenças finitas explícita, com um incremento de tempo de 600   s e um incremento no espaço de 30   m m .

Passo 1

Vamos lá! Nosso problema nos pede distribuição de temperaturas, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.

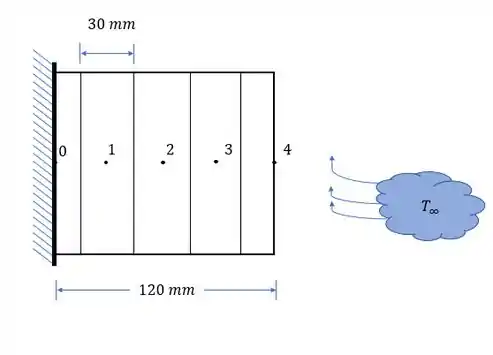
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - T r a n s f e r ê n c i a   u n i d i m e n s i o n a l

Passo 2

(a)

Vamos lá, a difusividade termal é dada por α = 1,6 ⋅ 10 - 6   ( m 2 / s ) , usando a equação 5.81 de diferença finita:

T m p + 1 = F o T m - 1 p + T m + 1 p + ( 1 - 2 F o ) T m p

Sendo F o dado por:

F o = α ⋅ Δ t Δ x 2 = 1,6 ⋅ 10 - 6   m 2 s ⋅ 600 s 0,03   m 2 = 1

Vale notar que o critério de estabilidade não é atendido pois 1 - 2 F o < 0 , assim.

Substituindo na equação 5.81 , temos:

T m p + 1 = T m - 1 p + T m + 1 p - T m p

Sendo a superfície em contato com o nó p = 0 , sendo adiabática e T 4 = T ∞ , vamos montar uma tabelinha para as nossas temperaturas.

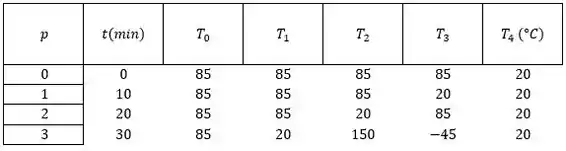
Temos que entender que essa tabela de temperaturas é irreal pois o critério de estabilidade não é satisfeito, assim é esperado que o resultado seja irreal.

Se fizermos a tabela para um intervalo de tempo menor que respeita o critério de estabilidade nossos dados seriam assim:

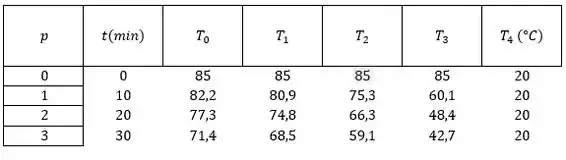
Isso é tudo pessoal! \o/

Resposta

(a)

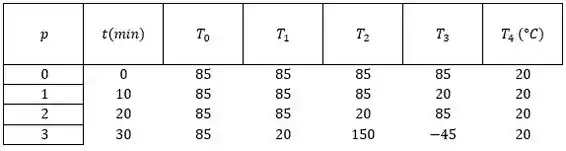
Dados irreais, justificativa vide passo-a-passo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma aleta plana triangular, bidimensional, com comprimento L = 50m m e espessura na base de t = 20m m . A condutividade térmica da aleta é k = 25W / m · K . A temperatura de sua base é T b =
47 – Canais quadrados de dimensão LC = 20,5(10 mm) = 14,14 mm são uniformemente espaçados em S=25 mm ao longo da linha central de um prato de espessura Lp= 40 mm. Fluido frio e quente escoam através d
113 – Uma chaminé passando gases quentes de exaustão tem uma área de seção transversal quadrada de 300 mm de lado. As paredes são construídas de tijolos refratários de 150 mm de espessura com uma cond
114 – Elementos de aquecimento elétrico de pequeno diâmetro dissipando 50W/m são usados para aquecer um prato de cerâmica de condutividade térmica 2W/m.K. A superfície de cima do prato está exposta ao
94 – A função Der(T,t) de IHT pode ser usada para representar a derivada temperatura-tempo da equação 5.75. Neste problema nós usaremos a função Der para resolver o Exemplo 5.12.(A) Mostre, usando o m