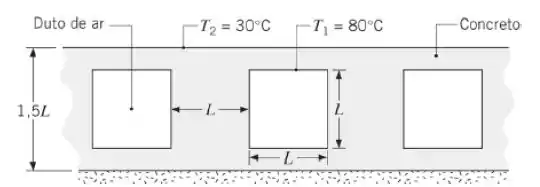
Um sistema comum para o aquecimento de uma grande área superficial consiste em passar ar quente através de dutos retangulares localizados abaixo da superfície. Os dutos são quadrados e posicionados na metade do caminho entre as superfícies superior e inferior, que estão exposta ao ar ambiente e isolada, respectivamente. Para a condição na qual as temperaturas do chão e dos dutos são de 30 e 80°C, respectivamente, e a condutividade térmica do concreto é de , calcule a taxa de transferência de calor saindo de cada duto, por unidade de comprimento do duto. Use uma malha com espaçamento de , com e L = 150 mm.

Boom galerinha, vamos começar?

Desenhando o que está acontecendo aqui:

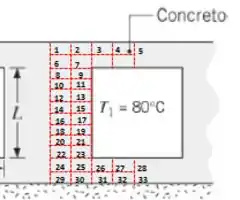
Ufaaa !! Foi difícil fazer e , mas deu certo !!

Nós queremos calcular a taxa de transferência de calor saindo de cada duto, como uma parte está isolada nós teremos que a condução para fora do tubo será:

Como

Já sabemos

Agora nós só precisamos das temperaturas, bora calcular?

Para todos os pontos nós temos um nó no interior, quando é assim nós podemos usar a fórmula:

Por isso se preparem que lá vem chumbo:

Quando resolvemos as equações simultâneas:

Substituindo no calor:

E acabou-se?

Claro que não kkkkk

Mas tá quase !! Precisamos lembrar que o duto é formado por duas partes iguais à que foi analisada, certo?

Se é assim a troca de calor total:

E acabamos mais uma galerinhaa !!