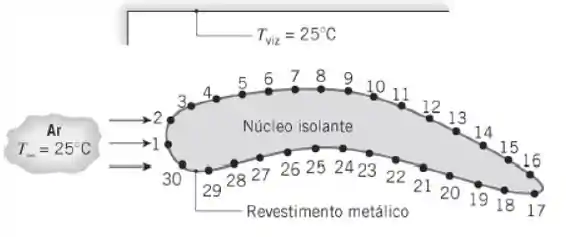
Considere usar a metodologia experimental do Problema 4.70 para determinar a distribuição de coeficientes de transferência de calor ao redor de um aerofólio de forma complexa.

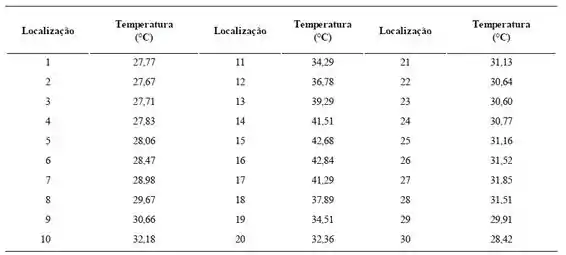
Levando em conta a condução através do revestimento metálico e perdas por radiação para a grande vizinhança, determine os coeficientes de transferência de calor por convecção nas posições identificadas. As posições na superfície nas quais a temperatura foi medida estão espaçadas de 2 mm. A espessura do revestimento metálico é t = 20 μm, a taxa de geração volumétrica é , a condutividade térmica do revestimento e a emissividade da superfície pintada é ε = 0,98. Compare seus resultados a situações nas quais (i) tanto a condução ao longo do revestimento quanto a radiação são desprezados, e (ii) quando somente a radiação é desprezada.

Vamos seguir galerinha??

Esse é lega !!! Bora animar aiii !!

Todos os nossos pontos sofrem condução dos pontos vizinhos e trocam calor por convecção e radiação:

Este é o nosso caso geral e chamaremos de Caso A.

No Caso B nós vamos desconsiderar a radiação:

E no Caso C nós vamos considerar apenas a convecção:

Nós já sabemos que:

Agora nós substituímos nossos dados nas fórmulas, certo?

Caso A:

Caso B:

Caso C:

Nós temos todas as temperaturas, certo?

Então é só substituir:

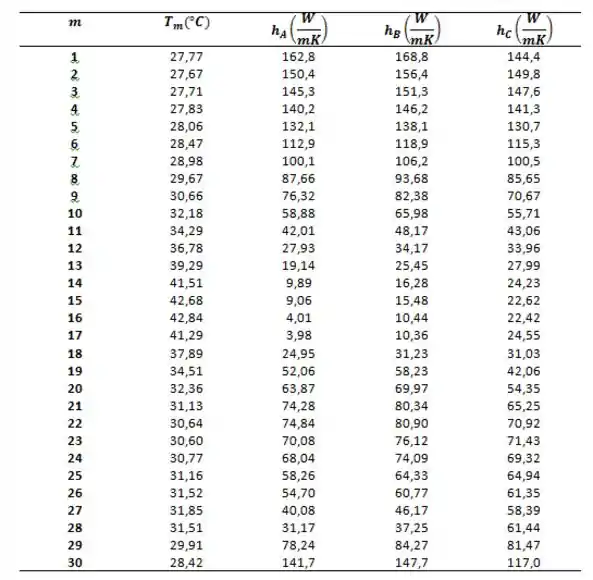
Quando fazemos a tabelinha fica fácil de observar as diferenças entre os três casos !!

E assim nós chegamos ao fim de mais uma !!