Movimento Relativo Unidimensional
Teoria
Imagina a seguinte situação, você está no ônibus indo para a faculdade junto com um amigo que está sentado no banco do seu lado. Vocês avistam uma amiga parada no ponto esperando o ônibus, mas o motorista passa direto no ponto sem parar a uma velocidade de . Qual é a velocidade do seu amigo no seu referencial? E no referencial da sua amiga, que está no ponto?
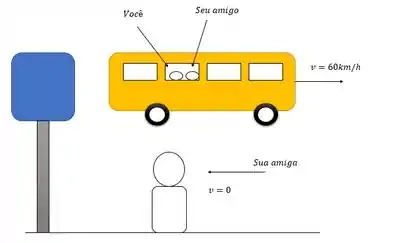
Aqui surge uma nova pergunta, com um novo conceito, o referencial.
Referencial
O referencial é a referência que você escolhe para o movimento ou seja, depende de quem observa.
Vamos voltar então para o exemplo do ônibus.
No seu referencial, ou seja, para você o seu amigo está sempre na mesma posição, que é do seu lado. O que isso quer dizer? Significa que ele está parado em relação a você.
No entanto, se usarmos a amiga de vocês como referencial, você e seu amigo passaram por ela com uma velocidade de . Para ela vocês estão se movendo.
Então tanto a velocidade quanto o deslocamento dependem do referencial.
Movimento Relativo
Quando utilizamos um referencial que não está parado, ou seja, com , chamamos o movimento do corpo estudado de movimento relativo, pois vamos estudar seu movimento relativo a outro corpo.
Ué, mas quando utilizamos um referencial parado, ainda sim não estamos fazendo um movimento relativo a esse referencial?? Sim, mas o movimento em relação a um corpo parado é o padrão e por isso damos o nome de movimento relativo o movimento em relação a um corpo em movimento.
No movimento relativo, podemos ter todos os dados relativos a um referencial. Quero dizer que podemos ter a posição relativa, a velocidade relativa e até aceleração relativa.
No exemplo de você e seu amigo no ônibus, temos que a posição dele em relação a você é zero, pois ele está do seu lado, mas em relação a menina no ponto de ônibus seria de alguns metros alguns segundos depois que o motorista passou pelo ponto.
A velocidade dele em relação a você é zero, pois ele está parado do seu lado, mas em relação a menina a velocidade dele seria .
Já a aceleração seria zero em ambos os referenciais, pois seu amigo não está variando a velocidade em nenhum dos referenciais.
Movimento relativo em uma dimensão
Pra entender o movimento relativo vamos começar com o movimento em uma dimensão, vamos dar uma olhada nesse exemplo:
Imagina que temos dois corredores com as velocidades indicadas na figura.
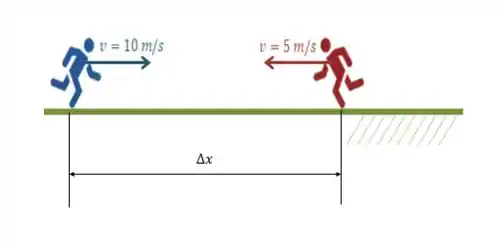
Com que velocidade o corredor azul se aproxima do corredor vinho (também conhecido como velocidade do corredor azul em relação ao corredor vinho)? Após calcular a velocidade, calcule também a posição relativa do corredor azul em relação ao corredor vinho para o tempo se o espaço entre eles é metros e a velocidade deles é constante.
De novo apareceu a expressão “em relação a”, isso quer dizer o que? Que vamos usar o que aprendemos de movimento relativo! Se liga no bizu:
Para calcular a velocidade relativa em uma dimensão, podemos usar a fórmula.
Onde é a velocidade do objeto em relação a um referencial parado, é a velocidade de em relação ao mesmo referencial e é a velocidade de em relação a .
Lembre sempre dos sinais do movimento unidimensional, o sinal DEVE entrar no valor da velocidade.
Como o corredor azul está correndo para direita e o corredor vinho para a esquerda,
Vamos usar a fórmula,
O corredor azul se aproxima com velocidade de .
E a posição? A gente calcula de forma bem parecida.
Onde é a posição do objeto em relação a um referencial parado, é a posição de em relação ao mesmo referencial e é a posição de em relação a .
Lembrando que:
E como a gente tá querendo a posição do corredor azul em relação ao corredor vinho, o nosso referencial está no corredor vinho, assim para o corredor vinho
O corredor azul começa na posição e se aproxima do corredor vinho, sendo assim seu espaço será dado por:
E como a velocidade tá no sentido oposto, o sinal deve entrar aqui!
Aplicando a fórmula para o ponto final teremos:
Podemos extender a fórmula que terminamos de aprender para aceleração.
Vamos agora praticar com alguns exercícios!!!
Movimento Relativo
Movimento relativo em uma dimensão
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 89-70.
Um barco está navegando rio acima, no sentido positivo de um eixo x, a 14 em relação à água do rio. A água do rio está correndo a em relação à margem. Quais são o módulo e a orientação da velocidade do barco em relação à margem? Uma criança no barco caminha da popa para a proa a em relação ao barco. Quais são o módulo e a orientação da velocidade da criança em relação à margem?
Passo 1
Nos itens e queremos saber a velocidade do barco em relação à margem do rio que é um referencial parado.
O problema nos fornece a velocidade do barco em relação a água do rio que é rio acima e também dá a velocidade do rio em relação à margem , negativo pois as águas do rio movimentam-se para baixo, sentido negativo.
A fórmula que temos é :
Substituindo os valores
Onde é a velocidade do barco em relação à margem do rio.
Passo 2
Queremos o módulo de
Passo 3
Como a velocidade do barco em relação à margem deu positiva, significa que o barco move-se no sentido para cima da margem, pois esse é o sentido positivo que o problema adota.
Passo 4
Nos itens e queremos saber a velocidade da menina em relação à margem do rio que é um referencial parado.
Acabamos de descobrir a velocidade do barco em relação à margem e temos a velocidade da menina em relação ao barco , positivo pois a menina caminha de trás (popa) para a frente (proa), ou seja, no sentido rio acima, nosso sentido positivo.
é a velocidade da menina em relação à margem, como o valor é positivo esse é o valor em módulo já.
Passo 5
A velocidade da menina em relação à margem deu positiva o que significa que ela move-se no sentido do rio acima, pois foi o sentido do movimento que o problema adotou como positivo.
Resposta
Rio acima
Rio acima
Exercício Resolvido #2
UFMS
Um carro move-se com velocidade constante de 60 km/h. Começa a chover e o motorista observa que as gotas de água da chuva caem formando um ângulo de 30° com a vertical. Considerando que, em relação à Terra, as gotas caem verticalmente, qual a velocidade em que as gotas de água caem em relação ao carro?
a) 30√3 km/h.
b) 60 km/h.
c) 120 km/h.
d) 30 km/h.
e) 80km/h.
Passo 1
Primeiro vamos entender o que ta acontecendo. A imagem mostra Vc como a velocidade do carro e Vr como a velocidade relativa da chuva em relação ao carro. O ângulo formado entre Vr e a reta na vertical é de 30°, então temos algo assim:
Como sabemos lá da trigonometria:
No nosso caso:
Resposta
c) 120 km/h.
Exercício Resolvido #3
CMais
Um barco com velocidade de 10 km/h em relação ao rio tenta ir de uma margem a outra. A velocidade da água em relação à Terra é de 5 km/h. Qual deve ser a velocidade do barco em relação à Terra para que ele cruze o rio perpendicularmente às margens?
Passo 1
Já que o rio tenta puxar o barco com sua velocidade da água e queremos atravessar o rio perpendicularmente, teremos algo assim:
Onde é a velocidade relativa do barco pro rio, é a velocidade relativa do barco pra terra e é a velocidade relativa do rio pra terra. Como a questão nos disse que é uma trajetória perpendicular ao rio, podemos utilizar pitágoras! Então, sabemos que:
Beleza! Agora é só substituirmos nossos valores:
Prontinho! Terminamos!
Resposta
Exercício Resolvido #4
FUVEST
Dois carros, A e B, movem-se no mesmo sentido, em uma estrada reta, com velocidades escalares constantes vA = 100 km/h e vB = 80 km/h, respectivamente.
- Qual é, em módulo, a velocidade do carro B em relação a um observador no carro A?
- Em um dado instante, o carro B está 600 m à frente do carro A. Quanto tempo, em horas, decorre até que A alcance B?
Passo 1
Temos dois carros se movimentando no mesmo sentido e com velocidades constantes, se liga na imagem.
A velocidade relativa do carro em relação ao carro será a mesma em módulo que a velocidade do carro em relação ao carro , como a questão só pede o módulo podemos calcular assim:
Sendo assim é só a gente substituir os valores e já era:
Passo 2
No item b, temos uma situação onde o carro está na frente do carro em , olha só:
Nesse caso aqui devemos fazer a velocidade do carro em relação ao carro , nós já até calculamos o módulo da velocidade relativa, mas vamos fazer aqui pra ver a questão do sentido.
E como as velocidades são constantes, podemos utilizar a equação da velocidade média lá do Movimento Uniforme! Então ficamos com:
Massss presta atenção nas unidades! A distância tá em metros e a velocidade em km/h, então, passando esses 600m pra km, temos 0,6km! Show, bora lá:
Prontinho! Terminamosss!
Resposta
Exercício Resolvido #5
UNESA
Dois trens partem simultaneamente de um mesmo local e percorrem a mesma trajetória retilínea com velocidades constantes, respectivamente, iguais a 300km/h e 250km/h. Há comunicação entre os dois trens se a distância entre eles não ultrapassar 10km. Depois de quanto tempo após a saída dos trens perderão a comunicação via rádio?
Passo 1
Bora pra mais umaaa!
Então na nossa situação temos dois trens partindo do mesmo lugar com velocidades diferentes, desse jetio aqui:
E queremos saber quando eles vão perder a comunicação, sabendo que a comunicação se perde quando eles estão 10km distantes entre si... Puts, complicou, né? Complicou nada rapá, tu tá com a gente do Responde Aí pra te ajudar :p
Se temos a velocidade e o sentido dos dois, podemos calcular a velocidade relativa entre eles e usar essa velocidade relativa pra sabermos em quanto tempo ela vai percorrer uma distância de 10 metros!
Então bora lá!
Calculando a velocidade relativa de mesmo sentido, temos:
Prontinho!
Passo 2
Nosso próximo passo é aplicar essa velocidade e a distância de 10 metros na equação do movimento uniforme, porque nossa velocidade é constante! Então vamo nessa:
Show, então o tempo pra eles estarem distantes 10km é 1/5 de hora! Mas quanto vale 1/5 de hora em minutos? Só multiplicar por 60, né?
Conseguimosss! Tu é fera!
Resposta
Exercício Resolvido #6
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 89-69
Um cinegrafista está em uma picape que se move para oeste a enquanto filma um guepardo que também está se movendo para oeste mais depressa que a picape. De repente, o guepardo pára, dá meia-volta e passa a correr a para leste, de acordo com a estimativa de um mebro da equipe, agora nervoso, de pé na margem da estrada, no caminho do guepardo. A mudança de velocidade do animal leva . Quais são o módulo e a orientação da aceleração do animal em relação ao cinegrafista e o módulo e a orientação da aceleração do animal em relação ao membro nervoso da equipe?
Passo 1
O problema quer a aceleração do guepardo um item em relação a um referencial e no outro item em relação a outro referencial. Para calcularmos essa aceleração vamos usar a formula
Pois o enunciado nos fornece o tempo e nos dá algumas velocidades, então precisamos apenas achar a velocidade de acordo com o referencial pedido no item para calcularmos a aceleração em relação aquele referencial.
Passo 2
Queremos a aceleração do guepardo em relação ao cinegrafista que está na picape, assim precisamos saber qual é velocidade inicial do guepardo em relação ao cinegrafista e sua velocidade final em relação ao cinegrafista.
A velocidade inicial o problema fornece ao dizer que a velocidade do guepardo é mais depressa, adotando o sentido oeste como positivo, temos que a velocidade do guepardo em relação ao cinegrafista é .
A velocidade final do guepardo em relação ao cinegrafista, vamos ter que calcular, pois temos apenas a velocidade do cinegrafista em relação a um referencial parado e a velocidade do guepardo em relação a um referencial parado também , negativo, pois o movimento é para leste, sentido negativo.
Agora vamos substituir na equação da velocidade para achar a aceleração do guepardo
Como a velocidade está em e o tempo em segundo, vou passar a velocidade para
Como queremos o módulo, temos que a aceleração do guepardo em relação ao cinegrafista é de .
Passo 3
A aceleração é negativa pois o guepardo passa a mover-se no sentido negativo do movimento, para leste.
Passo 4
Queremos a aceleração do guepardo em relação ao membro da equipe que está parado na estrada, assim precisamos saber qual é velocidade inicial do guepardo em relação ao membro da equipe parado e sua velocidade final em relação ao mesmo membro da equipe.
A velocidade final o problema diz que é de acordo com esse membro da equipe, temos que a velocidade final do guepardo em relação ao membro que é , negativo pois é no sentido de oeste para leste, sentido negativo do movimento.
A velocidade inicial do guepardo em relação ao membro da equipe, vamos ter que calcular, pois temos apenas a velocidade do membro que é zero, já que ele está parado. A velocidade do guepardo em relação a picape é , e a velocidade da picape é de
é a velocidade do guepardo em relação aum referencial parado, que é o membro da equipe na estrada. Assim podemos substituir na fórmula da velocidade em um MRUV
Chegamos na mesma equação do item e por isso sabemos que o módulo da aceleração é
Passo 5
E a orientação da aceleração é no sentido negativo do movimento.
Resposta
Sentido negativo do movimento, de oeste para leste.
Sentido negativo do movimento, de oeste para leste.
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 89-71
Um homem de aparência suspeita corre o mais rápido que pode por uma esteira rolante, levando para ir de uma extremidade a outra. Os seguranças aparecem e o homem volta ao ponto de partida, correndo o mais rápido que pode, levando . Qual é a razão entre a velocidade do homem e a velocidade da esteira?
Passo 1
Precisamos achar uma relação entre a velocidade do homem e a velocidade da esteira. Pela fórmula de velocidade relativa e função hóraria da posição podemos achar essa relação.
No primeiro movimento o suspeito percorre toda a esteira de comprimento em , assim podemos escrever a equação horária da posição
Onde é a velocidade do suspeito em relação a Terra no primeiro movimento. Como esse movimento foi o que gastou menor tempo e sabemos que nos dois movimentos o suspeito corria com velocidade máxima , temos que nesse movimento o suspeito corria na mesma direção que a esteira se movimentava. Por isso a equação de velocidade relativa fica.
Substituindo esse valor na equação da posição chegamos em
Passo 2
Já na hora de voltar, o mesmo homem gastou para percorrer a mesma distância
Onde é a velocidade do suspeito em relação a Terra, como esse movimento o suspeito corre contra o movimento da esteira ele gasta mais tempo, pois sua velocidade em relação a Terra é menor que no movimento anterior.
é negativa, pois é contrária ao movimento, já que adotamos o sentido da esteira como positivo.
Agora, substituindo essa velocidade na equação da posição achamos
Passo 3
Dividindo uma equação da posição do primeiro movimento pela outra temos
Resposta
Exercício Resolvido #8
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 84
Dois píers estão localizados em um rio: o píer está situado a de correnteza abaixo, como na figura. Dois amigos devem fazer um percurso do píer ao píer e depois voltar. Um deles vai de barco com velocidade constante de em relação à água. O outro caminha pela margem do rio com velocidade constante de . A velocidade do rio é igual a no sentido de para . Calcule o tempo de cada um para fazer o percurso de ida e volta.
Passo 1
Vamos começar calculando o tempo que o amigo faz caminhando. Basta usar a equação de velocidade média. Se sua velocidade é constante ela é igual a velocidade média.
O percurso de ida e volta tem o dobro da distância entre o píer e o píer .
Nesse problema usamos e em vez de e porque é mais fácil, nesse caso, passar a distância para , do que passar a velocidade de para .
Passo 2
Vamos achar agora o tempo do amigo que faz o percurso de barco.
Devemos achar o tempo da ida e o tempo da volta do percurso. Para isso precisamos da velocidade do barco na ida e na volta.
- IDA:
- VOLTA:
Passo 3
Vamos achar agora o tempo que ele demora a ir do píer ao píer .
Passo 4
Vamos agora achar a velocidade do barco na volta.
A velocidade do barco é negativa porque ele está indo para esquerda.
Passo 3
Vamos achar agora o tempo que ele demora a ir do píer ao píer .
O é negativo porque ele se desloca para esquerda.
Passo 4
O tempo total será,