Vetor Velocidade e Aceleração Instantânea
Produzido por Ludovic BeghinTeoria
Vetor Velocidade Instantânea
Velocidade instantânea é a velocidade da partícula naquele exato momento. Em um movimento unidimensional dizemos que a velocidade instantânea é a derivada da função posição. Isso também é valido para duas ou três dimensões, temos que o vetor velocidade instantânea é a derivada da equação do vetor posição.
Eita, mas como derivar um vetor?? Parece estranho né! Mas para nossa felicidade é bem tranquilo. Basta derivar suas coordenadas separadamente.
Como o vetor velocidade é derivada do vetor posição, pode-se dizer que o vetor deslocamento é a integral do vetor velocidade :
Para integrar um vetor iremos separar e fazer a integral coordenada por coordenada
Vetor Aceleração Instantânea
A aceleração é o quanto a velocidade varia no tempo. Assim como fizemos com o vetor velocidade instantânea, o vetor aceleração instantânea poder ser escrito como a derivada do vetor velocidade no tempo.
Como vimos, podemos escrever de outra maneira
Como o vetor aceleração é derivada do vetor velocidade, pode-se dizer que a variação da velocidade é a integral do vetor aceleração :
Para integrar um vetor iremos separar e fazer a integral coordenada por coordenada
Mantenha em mente que:
- Para achar o vetor deslocamento você deve integrar o vetor velocidade;
- Para achar o vetor velocidade instantânea você deve derivar o vetor posição;
- Para achar o vetor variação da velocidade você deve integrar o vetor aceleração;
- Para achar o vetor aceleração instantânea você deve derivar o vetor velocidade.
Agora que já relembramos o que conseguimos derivando ou integrando, vamos colocar em prática nosso conhecimento!
Vetor Aceleração Instantânea
Exercícios Resolvidos
Exercício Resolvido #1
USP
O vetor posição de uma partícula é dado por , em metros, para t medido em segundos. Para o instante , os vetores velocidade e aceleração dessa partícula se escrevem:
a)
b)
c)
d)
e)
Passo 1
Como queremos a velocidade a aceleração instantânea no momento de 2 segundos, a gente precisa lembrar que a derivada do espaço em função do tempo é a velocidade, e que a velocidade derivada em função do tempo é a aceleração! Então vamos lá:
No tempo de 2 segundos é só substituir o 2 no lugar do tempo na equação, ou seja:
Show!
Passo 2
Agora vamos calcular a aceleração, derivando a equação da velocidade dessa vez:
Fechamos!
Resposta
d)
Exercício Resolvido #2
USP-1ª Prova-2013
Sabendo-se que a posição de uma partícula, em relação à origem do plano , é determinada pelo vetor:
Com em metros () e em segundos (), determine:
O vetor velocidade instantânea e o vetor aceleração instantânea em função do tempo.
O vetor velocidade instantânea no ponto e o vetor aceleração instantânea no ponto , ambos os pontos estão indicados no gráfico abaixo. Neste gráfico, a curva contínua representa a trajetória da partícula, descrita através do vetor posição
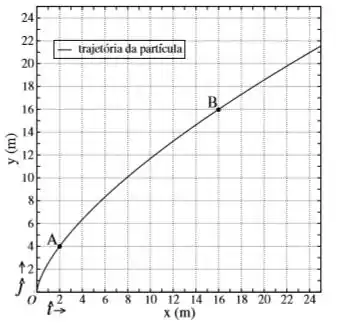
O vetor velocidade média e o vetor aceleração média , ambos entre os pontos e .
Passo 1
Lembrando que o vetor velocidade nada mais é do que a derivada do vetor posição, portanto:
E por sua vez, a aceleração é a derivada da velocidade, então:
Passo 2
Já possuímos as equações do vetor velocidade e aceleração, mas ambos estão em função do tempo. Então para utilizá-los precisamos do instante de tempo do ponto e do ponto . Para descobrir o tempo, basta substituir as coordenadas do ponto na equação da posição.
Igualando as componentes de e :
Ou
Logo, o ponto corresponde ao instante .
Fazemos o mesmo para o ponto .
Igualando as componentes de e :
Ou
Logo o ponto B corresponde ao instante .
Agora substituindo, temos que a velocidade instantânea no ponto é:
E agora o vetor aceleração instantânea no ponto
Passo 3
Bem, nós calcularemos a velocidade média com a fórmula:
E a aceleração média com a fórmula:
Observando ambas as fórmulas vemos que ainda nos falta calcular , e que são respectivamente, , e . Então, mãos a obra:
Show! Agora já temos tudo para calcular as médias.
Velocidade média.
Aceleração média.
Resposta
Exercício Resolvido #3
USP-1ª Prova-2012
O vetor posição de uma partícula que se move no plano é dado por:
Onde é dado em metros e em segundos. Determine:
O vetor velocidade instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;
O vetor aceleração instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;
O vetor deslocamento da partícula no intervalo de tempo até ;
O vetor velocidade média da partícula no intervalo de tempo até .
Dado:
Passo 1
O vetor velocidade instantânea pode ser obtido pela derivação do vetor posição em função do tempo, ou seja:
Portanto o vetor velocidade instantânea para vale:
E o módulo vale:
Já temos as componentes e , podemos fazer uma analogia em que a componente é o cateto oposto, e a componente é o cateto adjacente. E então utilizando relação trigonométrica encontramos o ângulo do vetor resultante com o cateto adjacente, ou seja, com o eixo . Então:
Passo 2
O vetor aceleração instantânea pode ser obtido pela derivação do vetor velocidade em função do tempo, ou seja:
O módulo do vetor para vale:
Sua direção é (paralela ao eixo ).
Passo 3
As posições para os instantes e valem:
Portanto o deslocamento é igual a:
Passo 4
A velocidade média entre os intervalos e é por definição igual a:
Agora é só jogar na fórmula:
Resposta
Exercício Resolvido #4
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 86-52- Modificado
Uma partícula tem uma aceleração constante . No tempo , a velocidade é zero e o vetor posição é . Encontre os vetores velocidade e posição em função do tempo . Encontre a equação da trajetória (de em função de ) da partícula no plano e esboce a trajetória.
Passo 1
O problema nos fornece a equação da aceleração de um partícula e nos pede os vetores velocidade e posição em função do tempo.
Como a variação da velocidade é a integral da aceleração e o vetor deslocamento é a integral da velocidade. Precisamos apenas integrar a equação da aceleração. Então vamos lá.
Passo 2
Primeiro vamos encontrar a equação da velocidade, integrando a aceleração
Substituindo os valores de , e o de que o enunciado diz ser zero.
Passo 3
Para achar o vetor posição devemos integrar a velocidade
Vamos substituir os valores que acabamos de encontrar e o valor de
Passo 4
Para acharmos a equação da trajetória temos que sumir com o tempo e deixar a equação de forma que fique em função de
Pela equação da posição que acabamos de encontrar tempos que a posição e a posição .
Se isolarmos o tempo na equação de , temos
Podemos substituir isso na equação de e assim achamos a relação entre e
Isolando para acharmos a equação da trajetória
A trajetória será uma reta no plano
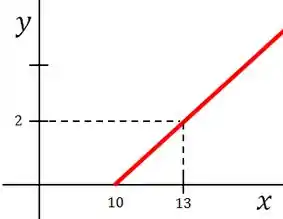
Resposta
Exercício Resolvido #5
Elaboração Própria
Uma partícula tem uma aceleração constante . No tempo , a velocidade é nula. Encontre o vetor velocidade em função do tempo .
Passo 1
O problema nos fornece a equação da aceleração de um partícula e nos pede o vetor velocidade em função do tempo.
Como a variação da velocidade é a integral da aceleração, precisamos apenas integrar a equação da aceleração. Então vamos lá.
Passo 2
Primeiro vamos encontrar a equação da velocidade, então:
Substituindo os valores de , e o de que o enunciado diz ser zero.
Resposta
Exercício Resolvido #6
UFPE 2018.2 1EE
A posição de uma partícula em metros é descrita pelo vetor posição .
Considere as afirmativas abaixo:
() A partícula passa pela origem do sistema de coordenadas.
() A tangente do ângulo entre o vetor velocidade e o eixo em é .
() O movimento da partícula não é acelerado.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Temos uma expressão para a posição da partícula em função do tempo. O único detalhe é que essa posição está sendo dada na forma de um vetor em e .
Vamos analisar cada afirmativa.
Passo 2
() A partícula passa pela origem do sistema de coordenadas.
Para que a partícula passe pela origem, basta que em algum instante de tempo a sua posição seja .
Então, vamos checar se isso acontece tanto em quanto em num mesmo instante.
Primeiro, vamos ver em quais instantes a partícula tem sua coordenada igual a zero:
Opaaa... achamos que a coordenada zera apenas em um instante de tempo negativo.
Como o tempo começa em , esse instante não existe.
A afirmativa () está incorreta.
Passo 3
() A tangente do ângulo entre o vetor velocidade e o eixo em é .
Vamos por partes.
Quem é o vetor velocidade?
Bom, a velocidade é a variação da posição, ou seja, sua derivada:
Agora, vamos descobrir o vetor velocidade no instante :
Agora, vamos calcular a tangente do ângulo que o vetor faz com a horizontal:
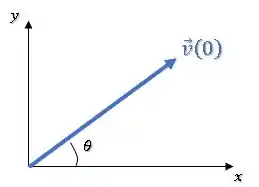
Para isso, basta usar as componentes em e em :
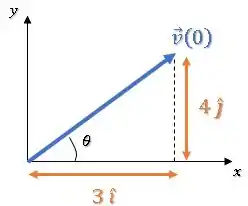
A afirmativa () está correta.
Passo 4
() O movimento da partícula não é acelerado.
Olhando para o vetor velocidade:
Podemos ver que ele varia, pois o termo da componente em tem um que vai alterar conforme o tempo.
Mas se quisermos ver explicitamente o vetor aceleração, basta derivar novamente:
Então, podemos ver que para todo instante de tempo após , há um vetor aceleração diferente de zero.
Assim, temos um movimento acelerado.
A afirmativa () está incorreta.
Temos apenas como correta, então, ficamos com a letra (b).
Resposta
Letra (b)
Exercício Resolvido #7
Elaboração Própria
Uma partícula movimenta-se em linha reta segundo a relação: , onde r é a distância, em metros e t é o tempo em segundos. Qual é a aceleração quando t=3?
Passo 1
Temos o vetor posição em função do tempo.
Para descobrir a velocidade em função do tempo, basta derivar:
E pra descobrir a aceleração em função do tempo, temos que derivar de novo:
Calculando a velocidade:
Derivando de novo pra encontrar a aceleração, temos:
Passo 2
Agora pra descobrirmos a velocidade no instante t=3, temos que substituir na equação que encontramos, então:
Prontinho!
Resposta
Exercício Resolvido #8
UFPE 2018.2 Editada
A posição de uma partícula em metros é descrita pelo vetor posição .
A velocidade e a aceleração instantânea da partícula em é
a)
b)
c)
d)
e)
f)
(g)
Passo 1
Temos o vetor posição em função do tempo.
Para descobrir o vetor velocidade em função do tempo, basta derivar:
E pra descobrir a aceleração em função do tempo, temos que derivar de novo:
Calculando a velocidade:
Derivando de novo pra encontrar a aceleração, temos:
Passo 2
O vetor velocidade no instante é:
O vetor aceleração no instante é:
Passo 3
Para achar a velocidade escalar, basta encontrar o módulo do vetor velocidade.
Nesse caso, fica bem fácil pois ele tem apenas a componente . Ou seja, seu módulo será a própria componente em :
Isso é igual à , e no caso da aceleração, temos:
logo ficamos com a alternativa (a).
Resposta
Letra (a)