Velocidade Vetorial
Produzido por Ludovic BeghinTeoria
Opaa, seja muito bem vindo ao Responde Aí! Bora conversar sobre Velocidade Vetorial?!
Vetor Velocidade Média em 2D
Aqui a gente vai aprender como calcular o vetor velocidade média quando o problema considera duas dimensões! Ou seja, agora a gente vai se movimentar com relação ao eixo
Siim, no movimento oblíquo a gente lida com a velocidade em duas dimensões. Afinal temos que considerar a velocidade no eixo
Existem duas formas de lidar com esse tipo de problema! Podemos calcular a velocidade média em cada dimensão ou usar diretamente a notação de vetor. Bora ver como isso funciona?!
📢 Clique para ver mais:
- Fórmula do Movimento Retilíneo Uniforme
- Fórmulas do Movimento Retilíneo Uniformemente Variado
- Fórmulas do Lançamento Oblíquo
Exemplo: Uma bola encontra-se na posição
Primeiro vamos calcular a velocidade média no eixo
Substituindo e calculando teremos:
Agora fazemos a mesma coisa para o eixo
Agora podemos escrever a velocidade da partícula em notação de vetor unitário:
Outra forma é calcular o vetor diretamente:
Como o tempo é um escalar essa divisão não é nenhum problema, o tempo vai dividir tanto as coordenadas de
Você também pode conferir esse conteúdo em vídeo:
Vetor Aceleração Média em 2D
O aceleração vetorial nos diz o quão rápido varia o vetor velocidade média no tempo, ou seja ele é a taxa de variação do vetor velocidade!
Assim como o vetor velocidade média ele também pode ser calculado eixo por eixo, isso é, podemos calcular a aceleração vetorial calculando a aceleração média do movimento em
Agora vamos praticar com exercícios?!
Vetor Aceleração Média em 2D
Exercícios Resolvidos
Exercício Resolvido #1
FMED Jundiaí
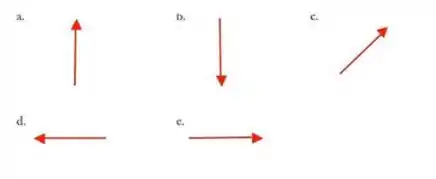
Ao se deslocar de sua casa (C) para faculdade (F), João Carlos faz o percurso esquematizado na figura, em que aparecem as velocidades vetoriais de partida () e de chegada () de seu movimento. Ambas as velocidades têm mesmo módulo. A aceleração vetorial média do movimento de João Carlos é melhor representada por:

a) ![]()
b) ![]()
c) Um vetor nulo.
d) ![]()
e)![]()
Passo 1
Se liga aí galera, nesse nosso caso não interessa o deslocamento tá? Vamos nos ater somente a velocidade, até por quê a aceleração média é dada pela seguinte equação:
Pra gente começar, vamos ver qual o sentido e direção de cada um dos vetores velocidade pra gente poder calcular a aceleração.
Passo 2
Se considerarmos ali o eixo horizontal sendo o eixo e o vertical o eixo , veremos que a velocidade aponta para baixo no eixo (Negativo) e a velocidade aponta pra direita no eixo (Positivo), em termos de vetores unitários temos então.
Onde representa o sentido negativo do eixo que por convenção é para baixo. E o sentido positivo do eixo que por convenção é para a direita.
E como a gente sabe, a aceleração média é dada por:
Então nossa aceleração tem uma componente em i e uma em j, sendo o vetor correto o da letra b, na diagonal, sendo a soma dos dois! Show!
Resposta
b) ![]()
Exercício Resolvido #2
UNICAMP
Um corpo viaja pelo caminho ilustrado na figura abaixon onde os vetores A e B são as representações das velocidades nos tempos e respectivamente.

Qual é o vetor que melhor representa a aceleração adquirida pelo corpo, entre os tempos e ?
Passo 1
Pela formulinha a gente sabe que:
Substituindo pelos dados do problema, a gente tem que:
Mas pra gente descobrir a direção e o sentido do vetor aceleração, nada melhor que a gente decompor esses vetores velocidade aí, né não? Como a questão só nos pediu a direção e o sentido, é só a gente analisar exatamente isso nos vetores velocidade, então, sendo o eixo x na horizontal e o y na vertical, a gente vê pelo desenho que:
Substituindo isso na nossa formulinha lá do começo, temos que:
Ou seja, nosso vetor tá apenas na direção do eixo x no sentido negativo, sacou? Show! Fechamos!
Resposta
![]()
Exercício Resolvido #3
Brasil Escola
Um carro move-se em linha reta a uma velocidade de 30 m/s. Ao avistar um obstáculo, o motorista faz uma curva brusca, alterando a direção da velocidade do carro para uma direção perpendicular, passando a se mover a 10 m/s. Admitindo que a curva foi realizada em um intervalo de tempo de 0,5 segundo, a aceleração vetorial média desse veículo foi de
a) 3√10 m/s²
b) 30 m/s²
c) √10 m/s²
d) 10 m/s²
e) 20√10 m/s²
Passo 1
Primeiro, vamos entender o percurso do problema:
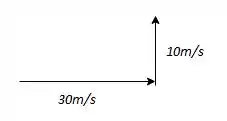
Como a gente viu, a aceleração média pode ser calculada por:
Agora é só a gente calcular o a velocidade resultante, como temos um triângulo, é só jogarmos pitágoras na parada, sacou? Então:
Passo 2
Agora que já temos o vetor resultante da velocidade, é só dividirmos pelo tempo, né? Então:
Showww!
Resposta
Exercício Resolvido #4
Elaboração Própria
Uma laranja possui as seguintes componentes vetoriais resultantes da velocidade: e .
- Determine o vetor velocidade resultante da laranja.
- O módulo do vetor velocidade resultante.
- A aceleração média sabendo que o tempo de percurso durou 5 segundos.
Passo 1
- Como a gente já viu, é só usar as coordenadas para representar os eixos respectivamente.
- Agora calculando o módulo da velocidade:
- Pra calcular a aceleração média, como a questão já nos deu o tempo, é só aplicar naquela formulinha:
Então o vetor velocidade fica:
Passo 2
Passo 3
Resposta
Exercício Resolvido #5
Só Física
Um corpo se desloca com velocidade , e aceleração constante , da forma como está descrita abaixo:
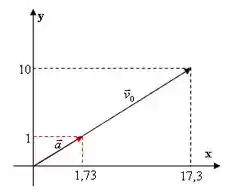
Qual é aproximadamente o vetor velocidade após 10 segundos?
Passo 1
Pra gente calcular a velocidade vetorial em função de um tempo, precisamos decompor os vetores velocidade inicial e aceleração em suas projeções em x e y, né? Então vamo lá:
Assim a gente pode dividir o momento em x em y, sacou? E no final usamos pitágoras pra calcular o valor absoluto do vetor Velocidade. Então, em x temos:
E em y:
Showww! Agora que a gente tem as duas componentes da velocidade em 10 segundos, podemos calcular o vetor resultante, né? Vem comigo:
Resposta
Exercício Resolvido #6
CocEducação
Uma partícula move-se em trajetória circular, com velocidade escalar constante de 10 m/s. A figura a seguir mostra suas passagens pelos pontos A e B, quando cumpre um quarto de volta em 2,0 segundos.
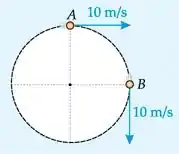
a) Essa partícula possui velocidade constante?
b) Determine o módulo do vetor que indica a variação de sua velocidade entre os pontos A e B.
c) Qual o módulo de sua aceleração média entre os pontos A e B?
Passo 1
Bom, essa letra a é bem pegadinha :p
A velocidade não mudou de valor, o que pode induzir você a achar que a velodidade é constante, mas nossa velocidade mudou de direção, tá vendo ali? Antes ela tava na horizontal, e depois foi pra vertical, então ela não é constante!
Passo 2
A gente tem a seguinte configuração vetorial:
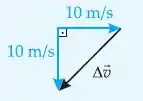
Show, né? É só a gente usar aquela regrinha:
Passo 3
E agora pra calcularmos a aceleração média tendo o tempo e a velocidade ficou moleza, né?
A partícula andou exatamente um quarto de volta, e no enunciado diz que o tempo desse movimento foi de 2 segundos! Vamo nessa:
Conseguimos! :D
Resposta
- Não.
Exercício Resolvido #7
Elaboração própria
Um avião parte do Rio de Janeiro com destino a Recife, porém ele possui uma escala em Brasília. O primeiro trecho, entre Rio de Janeiro e Brasília, possui e o avião demora nele. Em seguida, o avião fica parado em Brasília por para abastecimento e embarque/desembarque de passageiros. O segundo trecho, entre Brasília e Recife, possui e o avião demora para percorrê-lo. A figura abaixo ilustra o plano de vôo do avião. Determine o módulo, direção e sentido da velocidade vetorial média do avião do inicio do vôo, no Rio de Janeiro, até o fim do vôo, no Recife. Considerando como a origem do sistema cartesiano a cidade do Rio de Janeiro.
Dados: , ,,
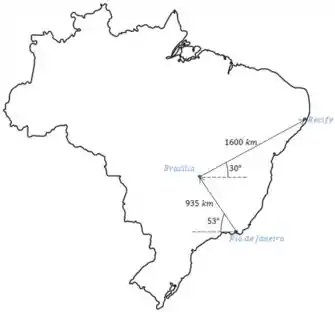
OBS: Pegue uma calculadora, você vai precisar !!!
Passo 1
Para calcular a velocidade média vetorial, devemos ter o deslocamento vetorial e o tempo total do percurso. Para isso devemos descobrir o deslocamento vetorial em cada trecho da viagem.
Vamos chamar de trecho 1 a parte Rio - Brasília e de trecho 2 a parte Brasília - Recife.
Passo 2
Primeiro vamos calcular o tempo total do percurso. Ele é a soma do tempo de vôo de cada trecho mais o tempo parado em Brasília.
Passo 3
Vamos achar agora os deslocamentos do trecho Rio – Brasília.
Para isso devemos decompor o vetor deslocamento entre as cidades, da mesma forma que fizemos no capítulo de vetores, atento ao sinal.
Usando a “regra do COlado/SEparado” teremos
.
Lembrando que para cima/para direita significa sinal positivo, enquanto para baixo/para esquerda significa sinal negativo.
Passo 4
Vamos achar agora os deslocamentos do trecho Brasília – Recife, da mesma forma que fizemos para o outro trecho.
Usando a “regra do COlado/SEparado” teremos.
Lembrando que para cima/para direita significa sinal positivo, enquanto para baixo/para esquerda significa sinal negativo.
Passo 5
Vamos agora achar o deslocamento total em cada direção,
Podemos escrever esse deslocamento da seguinte forma vetorial
Passo 6
A velocidade média vetorial pode ser calculada pela fórmula.
Escrever a velocidade média vetorial como vetor mostra a direção e sentido. Porém não o módulo.
Passo 7
O módulo de será,
Resposta
Exercício Resolvido #8
Elaboração própria
Uma ambulância está trafegando a em uma estrada. Em seguida, ela entra em uma curva, como indicado na figura, com sua velocidade na horizontal. Ao sair da curva, sua velocidade sofre uma mudança de direção, passando a fazer um ângulo de , como mostrado na figura. Determine o módulo, a direção e o sentido da aceleração vetorial média nesse trecho, sabendo que ela demora para fazer essa curva.
Dados: ,
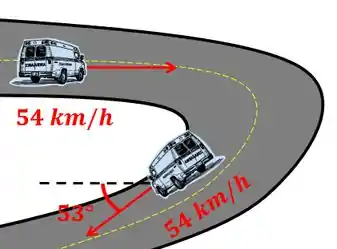
Passo 1
Para acharmos a aceleração vetorial média, podemos usar a fórmula.
Para usar a fórmula devemos, achar a variação do tempo e a variação da velocidade vetorial.
Passo 2
O valor de já temos pelo enunciado, só devemos colocar na unidade correta do SI.
Passo 3
Antes de qualquer coisa, devemos passar o módulo da velocidade de para .
Para isso vamos dividir o valor em por .
Passo 4
Devemos achar agora a variação da velocidade, para isso devemos achar a velocidade vetorial inicial e final. Nesse caso, como os vetores são simples, e o enunciado pede direção e sentido vamos fazer na forma vetorial direto. Começando pela velocidade inicial vetorial.
Passo 5
Agora vamos achar a velocidade final, para isso devemos achar suas componentes decompondo pelo seu módulo e ângulo como fizemos no capítulo de vetores.
Lembrando que para cima/para direita significa sinal positivo, enquanto para baixo/para esquerda significa sinal negativo.
Passo 6
Agora vamos achar ,
Passo 7
A aceleração vetorial média será,
Passo 8
Agora devemos achar o módulo da aceleração.