Empuxo
Teoria
O que é isso?
O que faz com que uma embarcação não afunde quando colocada na água?
O peso de um navio é na ordem de toneladas. Como é possível algo com este peso flutuar?
Explicação Física
A força que contrabalanceia o peso de um sólido total ou parcialmente imerso em um fluido é chamada de empuxo. É por causa dessa força que alguns objetos flutuam em fluidos.
Você também pode conhecer o empuxo como o Princípio de Arquimedes, que diz:
Todo corpo imerso em um fluido sofre ação de uma força (empuxo) verticalmente para cima, cuja intensidade é igual ao peso do fluido deslocado pelo corpo.
Um objeto imerso em um fluido vai sofrer ação da pressão hidrostática, certo? Aquela que depende apenas da altura. Observe a figura abaixo:
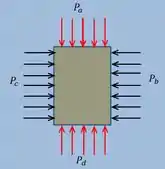
As pressões laterais se anulam, pois têm a mesma altura. Porém a altura da parte superior onde temos a pressão é menor que a altura de onde temos . Assim, lá de pressões hidrostáticas, vemos que .
A pressão é dada por:
Temos também que a pressão é:
A pressão resultante no corpo será a diferença entre e , que é:
Show? Bem, vimos que o empuxo era uma força e aqui encontramos uma diferença de pressão que aponta para cima. Vamos, colocar isso como uma força, lembrando que . Logo:
Agora, lembrando que , temos:
Sendo o volume do corpo que está SUBMERSO e a densidade do FLUIDO.
Além disso, outra forma de lembrar essa fórmula é notar que o empuxo é o peso do volume de fluido ocupado pelo sólido.
O peso de fluido é dado por:
Podemos usar esta outra forma, por que a massa é a densidade vezes o volume:
Só que o volume do fluido é o volume ocupado pelo sólido imerso:
Então o peso do fluido fica sendo o seguinte:
Como o empuxo é igual ao peso de fluido ocupado pelo sólido, então:
Observação 1: Como foi visto, o empuxo sempre apontará para cima, ou seja, contrário ao campo gravitacional, que aponta para baixo.
Observação 2: quando o peso do sólido é maior que o empuxo, temos uma resultante para baixo, e o sólido afunda. Quando o peso do sólido é menor que o empuxo, temos uma resultante para cima e o sólido sobe. Quando as forças são iguais, o sólido está em repouso.
Unidades
Para calcularmos o empuxo em Newtons (), precisamos colocar as seguintes unidades:
Peso aparente
Já pegou um amigo no colo dentro de uma piscina? Então você sabe como é bem mais fácil levantar alguém na piscina do que fora dela.
Por que isso acontece?
Há três forças agindo no corpo: seu peso, o empuxo e a normal.
O peso aparente é exatamente a força normal, ou seja:
É como se o empuxo estivesse “aliviando” um pouco a intensidade da normal.
Empuxo + Outra Força
Bom, agora que você já sabe o que é empuxo, vamos complicar um pouquinho o negócio: e se houver outra força atuando sobre o sistema?
Teremos dois casos gerais: o caso em que força tende a retirar o corpo do fluido e o caso em que a força tende a afundar ainda mais o corpo.
A forma de resolver cada questão vai sempre passar por um passo crucial: o equilíbrio de forças.
Vamos ver um exemplo:
O nome desse tipo de balança que usa uma corda é dinamômetro. Questões envolvendo dinamômetros são muito comuns nesse caso.
Beleza, como vamos montar o somatório de forças nesse problema?
Primeiramente, precisamos definir um sentido positivo para as forças: para cima ou para baixo.
No nosso caso, vamos dizer que o sentido para cima seja o positivo. Quais forças apontam para cima?
Se você respondeu: a tensão e o empuxo, você acertou (:
E qual força aponta pra baixo? Nesse caso, apenas o peso. Dessa forma, considerando o sistema em equilíbrio, temos:
E o que os enunciados costumam pedir?
Os enunciados podem pedir qualquer uma das três forças, dando informações sobre as outras duas.
Mas você deve prestar atenção em uma coisa: o peso aparente.
Lembra?
Definimos peso aparente como:
Ou seja:
Mas olhando de novo a nossa equação:
Ou seja: em questões envolvendo dinamômetros, a tensão da corda também poderá ser chamada de peso aparente!!
Sabendo disso, é só identificar cada força, montar a equação de equilíbrio, descobrir o que se quer e correr pro abraço!
Corpo na Interface de Dois Líquidos
Bom, mas como você vai calcular o empuxo quando a situação do problema for algo assim:
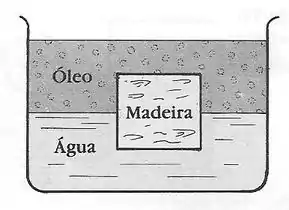
Aaah, te peguei!!! Tem dois líquidos ali, e cada um tem uma densidade diferente.
Como prosseguir então?
A forma certa de se pensar é considerar o empuxo total como a contribuição de dois empuxos:
Um agindo na parte superior do bloco, em contato com o óleo, e outro agindo na parte inferior, em contato com a água.
Como calcular o empuxo resultante?
Como vimos no tipo Empuxo, o empuxo sempre aponta para cima, assim:
E como se calcula cada empuxo? Sendo o volume do corpo dado por , teremos:
Assim:
Ficaria dessa forma, é claro, quando exatamente a metade do bloco está em cada fluido. Porém, se uma fração diferente de do volume bloco está em um fluido, teremos:
Sacou? Por exemplo:
A ideia é calcular cada um dos volumes submersos.
Bom, e se houver fluidos? E se o corpo estiver com uma certa parte do seu corpo dentro de cada fluido?
Ai teriamos um somatório assim:
Beleza?
Observação importante: Sempre será uma soma de empuxos, nunca uma subtração!
Vamos resolver umas questões agora (:
Unidades
Peso aparente
Empuxo + Outra Força
Corpo na Interface de Dois Líquidos
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercícios, Fenômenos de transporte
Um corpo rígido e não poroso, de volume e densidade é colocado em líquido de densidade , num local onde a aceleração da gravidade é de . O empuxo sofrido pelo corpo é:
Passo 1
O enunciado não informa se o corpo está completamente imerso no fluido ou não. O empuxo sofrido pelo corpo depende de quanto de água ele desloca, ou seja, de quanto ele afunda, lembra? Se o corpo ficar totalmente imerso no fluido, ele vai sofrer o empuxo máximo, pois vai deslocar o equivalente a todo o seu volume de fluido.
Vamos calcular como ficaria o empuxo máximo sofrido pelo corpo, como se ele estivesse completamente submerso. O empuxo é dado pela fórmula:
Sabemos a densidade do fluido:
Vamos supor que o objeto está totalmente imerso. Assim, também sabemos o volume imerso, que neste caso, é igual ao volume do objeto:
E a gravidade também é conhecida e fornecida pelo problema:
Passo 2
Agora vamos substituir na fórmula:
Vamos dar uma olhadinha nessas unidades?
Se liga:
Percebeu? Cortamos o com o . Agora, transformando pra
Já que :
Esse é o empuxo máximo sofrido pelo corpo. Isso quer dizer que, se o corpo estiver completamente submerso, esse será o valor do empuxo sofrido.
Passo 3
Precisamos agora descobrir se o corpo está totalmente imerso ou não. Pra isso, vamos calcular o peso do corpo:
Viu? Fizemos a mesma transformação que antes nas unidades.
Caramba! O peso do objeto é maior que o empuxo máximo que calculamos. Isso quer dizer que, mesmo que o corpo esteja completamente submerso, o empuxo não será maior que o peso.
Daí, podemos concluir que se colocarmos o corpo no fluido, ele vai afundar, e o empuxo sofrido por ele vai ser igual ao que a gente calculou no Passo 2! Ou seja, a resposta é a alternativa (d).
Resposta
Alternativa (d).
Exercício Resolvido #2
Elaboração própria
Um bloco de madeira cujo volume é está em repouso flutuando em água. Sabe-se que do volume do bloco está imerso na água.
- Qual é o valor da força de empuxo exercida no bloco?
- Qual é o peso do bloco?
- Qual é a massa do bloco?
- Qual é a densidade do bloco?
Considere que e
Passo 1
Resolvendo item (a):
O empuxo é dado pela fórmula:
Sabemos a densidade do fluido:
Agora podemos calcular o volume do bloco imerso na água:
Se o volume total é dado e igual a e desse volume está imerso, então podemos calcular o volume imerso:
E a gravidade também é conhecida e fornecida pelo problema:
Agora é só substituir na fórmula:
Passo 2
Resolvendo item (b):
Como o bloco está em repouso, o somatório de forças que agem no bloco deve ser nulo.
Neste caso, temos o peso para baixo e empuxo para cima. Logo, essas forças devem ser iguais:
Passo 3
Resolvendo item (c):
Como sabemos o peso, podemos calcular a massa do bloco:
Substituindo:
Passo 4
Resolvendo item (d):
Para calcular a densidade do bloco, precisamos da massa e volume, que já conhecemos!
Portanto:
Resposta
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 99 – Modificado
Uma bola de plástico de raio igual a flutua em repouso na água com de seu volume submerso.
- Que força você precisa aplicar à bola para mantê-la em repouso completamente abaixo da superfície da água?
- Se você soltar a bola, qual vai ser a aceleração dela no instante em que a soltar?
Dica: Volume de uma esfera de raio :
Dados:
Densidade da água:
Gravidade:
Passo 1
a)
Bom, temos aqui um problema que envolve três forças. Quais são elas?
O Peso, o Empuxo e a Força externa.
Abaixo podemos ver um esquema dessas três forças atuando no corpo( A força azul é o peso, a verde o empuxo e a vermelha a força externa):
Opa, mas essa é a formação final do sistema, certo?
E no início? Bem, no início o corpo estava apenas flutuando na água com de seu volume submerso. Isso é, havia apenas o empuxo e o peso no início:
Passo 2
Bom, vamos ter que analisar a situação inicial antes de partir pra luta. Por que? Porque precisamos saber o valor do peso da bola pra calcular a força que devemos aplicar.
No início, só havia o peso e o empuxo. A bola estava em equilíbrio, flutuando, o que nos leva a:
O empuxo inicial é o empuxo causado por do volume do corpo, ou seja:
Notou ali em cima o fator multiplicando o volume? Justamente, porque tem apenas do volume abaixo da água. Assim:
Passo 3
Agora podemos calcular a força que devemos aplicar quando todo o volume está submerso.
Quando todo o volume está submerso, o empuxo é máximo e vale:
Então, olhando a direção de cada força na figura que vimos no primeiro passo, teremos o seguinte somatório de forças( que precisa ser nulo de novo, já que o corpo está novamente em repouso):
E essa é a resposta da letra a).(:
Passo 4
b):
Agora imagine que você retire a força que dava equilíbrio pro sistema. Vamos ter uma força resultante diferente de zero e que vai gerar uma aceleração, certo?
Essa força é dada por:
Mas não sabemos a massa da bola, certo?
Bom, mas sabemos o peso. Ai fica fácil:
Assim, a aceleração será:
Uma bela aceleração, não é mesmo?
Resposta
a):
b):
Exercício Resolvido #4
E5.UFRJ-P1-2012.2-4
Um objeto de densidade está boiando num fluido de densidade quando este se encontra à temperatura . O fluido é então resfriado para a temperatura , causando um aumento em sua densidade, que agora vale . A densidade do objeto não se altera com o resfriamento. Sabendo-se que a fração do volume do objeto fora do fluido à temperatura é , qual a nova fração , agora à temperatura ?
Passo 1
Uma questão sobre empuxo. A maior complicação aqui é entender o que se conserva mesmo com a mudança de temperatura e como manipular as expressões pra conseguir o que se quer.
Bom, primeiro vamos entender como se calcula essas frações que o problema pede.
Como a fração diz respeito ao volume que se encontra fora do fluido, ela tem que ser a fração do volume total menos o volume deslocado pelo objeto. Isso é:
Ou de forma mais simpática
Por exemplo, se o corpo tem um volume que vale ,e tem unidades dentro do líquido, o volume exposto vale 2. Assim,
Passo 2
Quando a temperatura vale , na situação de equilíbrio o peso equilibra o empuxo e:
Agora a fração do volume do objeto fora do fluído é dada por
Beleza!
Passo 3
No segundo caso, quando a temperatura vale , a fração do fluído vai de parar , ou seja, a equação para a fração do volume do sólido fora do fluído é a mesma que achamos no item anterior só que mudando a densidade do fluído!
Lembrando que a densidade do sólido não mudou!
Passo 4
Olhando as nossas opções temos que relacionar com ! Para fazer isso, vamos isolar na equação de e jogar na equação para !
Saca só como vai ficar:
Agora é só jogar na equação de e partir para o abraço!
Que é a letra E de EIIITTAA NÓÓÓIIISSS!!!
Resposta
e)
Exercício Resolvido #5
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 95 – Modificado
Um lingote de alumínio sólido pesa no ar.
- Qual é o seu volume?
- O lingote é suspenso por uma corda leve e totalmente imerso na água. Qual é a tensão na corda (O peso aparente do lingote na água)?
Passo 1
a):
Bom, o peso do corpo é:
Assim, a massa será:
Assim, usando:
Passo 2
b):
Bom, agora o corpo será imerso na água. Isso quer dizer que surgirá um Empuxo no sistema.
Como vimos, a equação para esse caso será:
E essa tensão será o peso aparente do corpo.
Calculando o empuxo:
Passo 3
Assim, a Tensão será:
E esse será o peso aparente.
Resposta
a)
b)
Exercício Resolvido #6
PUCRIO-P1-2013.2-letras c, d
Um béquer com água tem massa total de e está em repouso sobre um prato de balança. Um bloco de alumínio de , suspenso por um dinamômetro, é totalmente mergulhado na água do béquer, como mostra a figura ao lado. (massa específica do alumínio: , massa específica da água: )
c) Determine a leitura do dinamômetro, calibrado em
d) Determine a leitura da balança, em
Passo 1
c):
Bom, galera, aqui a gente vai precisar montar a equação que rege todas as forças que agem sobre o bloco. As forças são: o peso, o empuxo e a tensão (que é o que o dinamômetro mede).
É isso! Achando a tensão, acharemos a resposta.
Primeiro temos que apontar as forças. Tanto o empuxo quanto a tensão apontam pra cima, enquanto o peso pra baixo.
Como o bloco está em equilíbrio, a soma das forças dará zero:
Então a nossa tensão fica
Vamos calcular essas duas forças!
O peso é fácil, pois o enunciado já nos deu a massa:
Passo 2
O Empuxo é dado por:
Mas não sabemos . No entanto, temos a densidade do alumínio e a sua massa. Assim, fica fácil encontrar o volume por ele deslocado:
Ok! Então voltando para a tensão
E finalmente
Beleza! Essa é a calibração do dinamômetro!
Passo 3
d):
A balança mede a Normal, certo? E qual Normal? É a Normal entre o bequer com água e a balança. Como o béquer está em equilíbrio basta apontar as forças nele.
Ué?!?!?!?! Empuxo apontando para baixo?! Pode isso, Arnaldo?!
A regra é clara! Se tem um empuxo sobre o bloco de alumínio produzido pela água no béquer, pela terceira lei de Newton, tem que ter uma força de reação com mesma intensidade, só que no sentido oposto!
Ah tá! Então esse empuxo pra baixo é a reação do bloco sobre o liquido! Beleza, então! Segue jogo!
Então usando a condição de equilíbrio
E finalmente!
Isso aí!
Resposta
c):
d):
Exercício Resolvido #7
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 95 – 26 Modificado
Um bloco de gelo flutua sobre um lago de água doce. Qual deve ser o volume mínimo do bloco para que uma mulher de possa ficar em pé sobre o bloco sem molhar os pés?
Dados:
Passo 1
O volume mínimo pra que o bloco consiga sustentar a mulher é aquele em que todo o volume submerso gera o empuxo necessário para a sustentação dela.
Sacou? Existe um volume de um bloco que, quando está totalmente submerso, gera um empuxo que sustenta a mulher sem que ela molhe os pés.
Passo 2
Como vimos na teoria, esse é um caso de uma força que tem de afundar o corpo. Assim, a equação para esse caso será:
Onde é o peso da mulher:
Passo 3
Vamos calcular os dois pesos:
O peso da mulher será dado por:
Passo 4
E o peso do gelo? Bem. Ele pode ser escrito como:
E o empuxo será dado por:
Assim, aplicando na equação anterior:
Assim:
Pronto (:
Resposta
Exercício Resolvido #8
PUCRIO-P1-2012.2
Uma esfera oca de ferro () é mantida submersa em um lago de água doce () amarrada a uma corda presa no fundo do lago. O raio externo da esfera é igual a . A tensão na corda é igual a . Considere .
Desenhe o diagrama de forças que atuam sobre a esfera.
Calcule a força de empuxo exercida pela água sobre a esfera.
Qual é a massa da esfera?
A corda se rompe e a esfera sobe até a superfície. Quando ela atinge o equilíbrio, qual é a fração do volume que fica submersa?
Calcule a espessura da casca esféria?
Passo 1
Para desenhar o diagrama de forças que atuam na esfera, vamos primeiro determinar que forças são essas!
As forças que atuam na esfera são:
- Força peso
- Empuxo
- Tração da corda
O diagrama de forças vai ficar assim:
Passo 2
Pela definição de empuxo, lembramos que ele é igual, em módulo, ao peso do volume de líquido deslocado, ficou confuso?! Se liga que a fórmula, é a seguinte:
Para o caso da esfera, temos que o volume imerso é dado por:
O empuxo fica:
Passo 3
Para determinar a massa da esfera, devemos calcular através do equilíbrio. Sabemos que por estar em equilíbrio, temos a seguinte relação:
Obs: Você deve estar pensando que é mais fácil achar a massa da esfera multiplicando a densidade pelo volume...mas...não é bem assim. Por se tratar de um esfera oca, não sabemos o volume de ferro presente na casca esférica, por isso tivemos que calcular a massa através da relação de equilíbrio.
Passo 4
Na nova situação de equilíbrio, não teremos mais a tração atuando, a relação de equilíbrio vai ser então:
Onde é a nova força de empuxo.
O novo volume imerso vai ser:
A fração do volume total que está submersa vai ser então:
Passo 5
Como sabemos a massa de ferro presente na esfera, assim como a densidade do ferro e o raio externo da esfera, podemos determinar a espessura da casca esférica. Se liga!
Pela definição de densidade, temos:
Onde é o volume de ferro da casca esférica, seu valor é:
Agora que temos o volume, podemos calcular o raio interno , tendo em vista que o raio externo foi dado!
Substituindo os valores, temos:
A espessura da casca é dada por:
Resposta
Ver figura acima
Exercício Resolvido #9
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 95 – Modificado
Um bloco de madeira cúbico com aresta de flutua sobre uma interface entre uma camada de água e uma camada de óleo, com sua base situada abaixo da superfície livre do óleo. A densidade do óleo é igual a ³ e a da água
- Qual é a pressão manométrica na face superior do bloco?
- Qual a pressão manométrica na face inferior do bloco?
- Quais são a massa e a densidade do bloco?
Passo 1
a):
Bom, como sabemos a distância da superfície livre do óleo até a face superior do bloco, sabemos a altura da coluna de fluido acima dele. Assim:
Assim:
Passo 2
b):
Olhando a nossa figura, podemos ver que a camada de óleo tem
E a camada de água?
Ela tem , já que o cubo afundou em relação à superfície do óleo (como diz o enunciado).
Assim, a pressão na face inferior vai ser a soma das pressões causadas pela coluna de óleo e pela coluna de água:
Passo 3
Como o corpo está em equilíbrio, podemos dizer que:
E esse empuxo seria:
Você pode estar pensando: Bora calcular cada um desses empuxos!
Porém, existe uma forma mais fácil: Lembra que o empuxo é a força causada pela diferença de pressão entre as faces superior e inferior? Pois bem, podemos dizer que:
Sendo que a área da face do cubo vale:
Assim:
Assim:
E a densidade? Bom, já temos a massa, só calcular o volume e aplicar a fórmula.
Assim:
Resposta
a):
b):
c):
Exercício Resolvido #10
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 99 – Modificado
Um bloco cúbico com densidade e aresta de comprimento flutua sobre um líquido de densidade maior .
a) Qual fração do volume do bloco fica acima da superfície do líquido.
b) O líquido é mais denso do que a água (densidade igual a ) e não se mistura com ela. Derramando-se água sobre a superfície do líquido, qual deve ser a camada da água para que a superfície livre da água coincida com a superfície superior do bloco? Expressa a resposta em termos de , , e . Calcule a profundidade da camada da água de parte (b) se o líquido for mercúrio e o bloco for de aço com aresta de 10,0 cm.
Dados:
Passo 1
a):
Vamos escrever as expressões pro peso e pro empuxo:
E pro peso:
Como o bloco está em equilíbrio, podemos igualar as forças:
Pronto, essa é a fração do volume que fica submerso. Pra descobrir qual é a fração que fica acima da superfície livre, basta subtrair isso do 1:
Passo 2
b):
Bom, nessa nova situação vão existir dois empuxos: Um causado pela água e um causado pelo fluido. Além disso, a configuração espacial do problema vai ficar assim:
Como você pode ver, a camada de água, o que queremos descobrir, é representada por . A camada de água coincide com a superfície do bloco.
Assim, o volume submerso na água será dado por:
E o volume submerso no fluido vai ser dado por vezes a área:
Passo 3
Show? Como esse novo sistema também está em equilíbrio, podemos dizer que a soma dos empuxos será igual ao peso:
Lembrando que:
Cortando nos dois lados:
Como e , o denominador e o numerador vão ser negativos, então vamos multiplicar ambos por
Calculando para o aço e o mercúrio:
Resposta
a):
b):
Exercício Resolvido #11
PUCRIO-P1-2012.1
A figura abaixo mostra duas bolas de mesmo raio, , imersas num recipiente contendo dois fluidos de densidades diferentes, óleo e água, cujas densidades são e , respectivamente. Estas bolas estão ligadas por um fio fino de massa desprezível. A bola está com metade de seu volume submerso em óleo e a outra metade em ar, e a bola , que é vezes mais densa que a bola , está com metade de seu volume submerso em óleo e a outra metade em água. As respostas deverão ser dadas no Sistema Internacional de unidades.
- Desenhe o diagrama de forças que atuam sobre a bola e sobre a bola . Despreze o empuxo do ar presente na parte superior do sistema.
- Encontre as densidades das bolas e ( e ).
- Encontre as massas das bolas e .
- Encontre a tração no fio.
Passo 1
a): Bom, as forças que atuam sobre cada bloco são: A tração, o peso e o empuxo.
Então:
Pra primeira bolinha (1):
Pra segunda bolinha:
Observação: A segunda bolinha está em contato com dois fluidos: A água e o óleo. Então, o empuxo que ela sofre é a soma dos empuxos dos dois fluidos. Fique atento a isso!
Passo 2
b):
Beleza, agora queremos achar a densidade de cada uma. Pra isso, como o sistema está em equilíbrio, vamos precisar montar a equação de equilíbrio das forças de cada uma:
Pra primeira:
Pra segunda:
Notou? O segundo empuxo vale:
Ok, mas esse sistema ainda tem incógnitas demais. O enunciado nos diz que a segunda bola é 6 vezes mais densa que a primeira. Então, por causa dessa informação, vale a pena reescrever o sistema passando a descrever os pesos com as densidades:
Passo 3
Com isso nosso sistema vira:
Subtraindo a segunda da primeira gente consegue eliminar e fica com
Dá pra cortar esse montão de e !!!
Agora isolando
Vamos converter os valores das densidades para (Basta multiplicar por 1000):
Então:
Como
Passo 4
c):
Tendo as densidades das bolas, é fácil descobrir a massa de cada uma. Podemos calcular o volume das esferas, já que temos o raio. O volume de uma esfera é dado por:
Sendo
Então:
E:
Passo 5
Isolando em alguma das equações, como nessa:
Resposta
a):
Pra primeira bolinha (1):
Pra segunda bolinha:
b):
c):
d):
Exercício Resolvido #12
E4.UFRJ-P1-2014.2-8
Uma bola é presa ao fundo de um recipiente, cheio de um líquido incompressível, por um barbante que se mantêm tensionado. Em seguida, o barbante se rompe, de modo que a bolinha passa a boiar sobre o fluido, conforme a figura. Sobre o nível do fluido nessas duas ocasiões, é correto afirmar:
- O nível do fluido não se altera após a ruptura do barbante, pois a densidade média da bola é igual à do fluido.
- O nível da água fica mais alto após a ruptura do barbante, pois a densidade média da bola é menor que a do fluido.
- O nível da água fica mais baixo após a ruptura do barbante, pois a densidade média da bola é menor que a do fluido.
- O nível da água fica mais baixo após a ruptura do barbante, pois a densidade média da bola é maior que a do fluido.
Passo 1
Antes de fazermos a questão, vamos pensar nessa situação:
Imagine uma bacia com água. O nível tem uma altura . Então, a gente joga uma bola nessa bacia que desloca um volume de água.
O que acontece com o nível e água?
Ele sobe ou desce?
Bem, se deslocamos o volume de água e no lugar daquela água toda colocamos um objeto, fica claro que o nível sobe pra uma altura . É como se você entrasse numa banheira pra tomar banho e a água “subisse”. Você ta ocupando o espaço que era da água, né?
Passo 2
Show, mas e ai? Bem, vamos analisar bem o problema:
Ele nos diz que a corda está tensionada de inicio. Isso quer dizer que existe uma força apontando pra cima, o empuxo, que é maior que o peso da bola. Mas isso significa que a densidade do fluido é maior que a densidade do corpo?
Sim, pois o empuxo é dado por:
E o peso é dado por:
No caso da figura 1, todo o corpo está submerso, então: . Então, como a resultante das forças aponta na direção do empuxo:
Então a densidade média da bola é menor que a densidade média do fluido.
Passo 3
Mas o que acontece com o nível? Bem, ai é só a gente lembrar da explicação inicial. Como todo o corpo estava antes submerso, ele havia deslocado um volume que gerou um nível .
Na situação 2, no entanto, parte do corpo passa a ficar exposto ao ar. Isso quer dizer que o volume deslocado agora, , é menor que o volume inicial
A consequência disso é que o novo nível vai ser menor que o nível inicial,
Então o nível vai ficar mais baixo!
Então a resposta é c).
Resposta
c)