Teoria
Incerteza
Todas as medidas possuem uma incerteza. Quando vamos medir uma mesa e falamos que ela possui está errado. Por conta das limitações dos instrumentos de medida, não se pode afirmar com exatidão a precisão das medidas, por isso, sempre colocamos uma incerteza na qual o valor poder estar contido. Quanto menor for a incerteza de uma medida, mais precisa ela é.
A incerteza de um número nem sempre é apresentada explicitamente, podendo ser representada pela quantidade de algarismos significativos de um número. Dissemos que a medida da medida da capa de um livro forneceu o valor , que possui três algarismos significativos.
Com isto aí, queremos dizer que os dois primeiros algarismos são corretos, enquanto o terceiro dígito é incerto. O último dígito está na casa dos centésimos, de modo que a incerteza é aproximadamente igual a .
Acurácia e precisão
É importante saber a definição de dois conceitos: acurácia e precisão
Acurácia: proximidade da medida relativamente ao verdadeiro valor da variável.
Precisão: proximidade entre os valores obtidos pela repetição do processo de mensuração.
Para explicar a diferença entre esses dois conceitos, eu gosto muito de pensar em um pênalti!
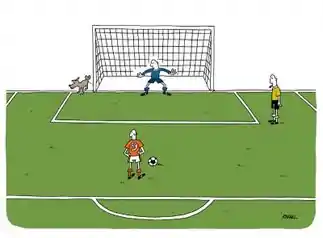
Quando um jogador é preciso?
Se o jogador bater o pênalti sempre na trave, no mesmo local, durante várias vezes, ele é muito preciso, porém pouco acurado. Ele é preciso, pois seus chutes sempre ficam no mesmo local, porém pouco acurado, pois seu objetivo, o gol, ele não faz.
Quando um jogador é acurado?
Se o jogador bate o pênalti e sempre faz o gol, porém em cada chute ele faz gol em lugar diferente, ele é muito acurado, porém pouco preciso. É acurado, pois sempre faz seu objetivo, porém pouco preciso, pois cada chute está em um local diferente.
Quando um jogador é acurado e preciso?
Se ele for um Pelé que nasceu com alegria nas pernas e sempre chuta no ângulo direito fazendo gol em todos os chutes, ele é acurado e preciso, pois sempre consegue fazer o gol chutando no mesmo lugar!
Acurácia e precisão
Exercícios Resolvidos
Exercício Resolvido #1
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 27 – 1.11.
Em uma competição com três arqueiros, cada arqueiro atira quatro flechas. As quatro flechas de José ficam a para a direita, para a esquerda, abaixo e acima do alvo. Todas as quatro flechas de Mário ficam dentro de um círculo de de raio com centro a do alvo central. Todas as quatro flechas de Flávio ficam a do alvo central. O juiz afirma que um dos arqueiros é acurado, mas não é preciso, outro é simultaneamente preciso e acurado, e o outro é preciso, mas não é acurado. Identifique os arqueiros que se enquadram nessas descrições e explique seu raciocínio.
Passo 1
Mário -
Por que preciso ?
Mario conseguiu acertar todas as flechas em um circulo pequeno, porém longe do alvo central desejado. Ou seja, todos os alvos foram localizados em um local, mas não no local ideal.
Passo 2
José –
José acertou as flechas em locais com a mesma distância do alvo central, porém em pontos diferentes, por isso a falta de precisão. A exatidão das flechas foi igual, todas à do alvo.
Passo 3
Flávio – Acurado e preciso
Todas as flechas ficaram próximas do alvo, ou seja, foi acurado e por ficarem juntas ele também foi preciso.
Resposta
Mário -
José –
Flávio – Acurado e preciso
Exercício Resolvido #2
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 28 – 1.13.
A figura mostra o resultado de um desastre provocado pelo erro inaceitável na posição final de parada de um trem.
- Suponha que o trem tenha percorrido de Berlim até Paris e tenha ultrapassado em o limite final do trilho. Qual o erro percentual na distância total percorrida ?
- Seria correto dizer que ele percorreu uma distância total de Explique

Passo 1
Para calcular o erro percentual precisamos fazer em relação à distância total percorrida.
Passo 2
Alternativa a)
Para calcular o erro precisamos saber quanto o erro representa da distância total.
Passo 3
Alternativa b)
É errado falar que a distância total percorrida é , pois essa distância também inclui o erro. O erro não faz parte da distância total realizada, pois os a mais não foram realizados como uma distância em cima do trilho.
Resposta
Alternativa (a)
Alternatva (b)
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 29 – ex1.16
Uma placa retangular de alumínio possui comprimento de e largura de .
- Ache a área do retângulo e a incerteza na área.
- Verifique se a incerteza fracionária na área é igual à soma das incertezas fracionárias do comprimento e da largura.
Passo 1
Em física nos sempre temos incertezas na mensuração. Para calcular a incerteza do retângulo vamos calcular os possíveis valores de largura e comprimento do retângulo.
Passo 2
Alternativa a)
Vamos ver os valores máximo e mínimo possíveis da largura e do comprimento e buscar ver os valores entre os quais a área do retângulo varia.
Para calcular as possíveis áreas do retângulo temos:
Calculando as possíveis áreas:
Assim, obtemos os valores médios e a amplitude máxima e mínima da área
Sendo que a área varia de (que é aproximadamente ) até (que é aproximadamente ), e por isso o erro será de . Assim:
Passo 3
Alternativa b)
Calculando as incertezas fracionárias
Incerteza da área:
Calculando as incertezas de comprimento e largura:
Sua soma vai ser , que é aproximadamente a incerteza na área.
De fato, se somássemos direto as razões, veríamos que essa soma é exata.
Só não observamos isso tão bem por causa dos arredondamentos na percentagem, mas se olhássemos todas as casas decimais, veríamos melhor como isso é válido.
Resposta
Alternativa a)
Alternativa b)
Incertezas:
A soma das incertezas do comprimento e da largura vão ser exatamente a incerteza da área.
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 34 –ex1.98
O comprimento de um retângulo é dado por e sua largura é .
- Mostre que a incerteza na área é dada por . Suponha que as incertezas sejam pequenas, de modo que o produto é muito pequeno e pode ser desprezado.
- Mostre que a incerteza fracionária na área é igual à soma da incerteza fracionária do comprimento com a incerteza fracionária da largura.
- Um paralelepípedo possui dimensões Ache a incerteza fracionária do seu volume e mostre que ela é igual à soma das incertezas fracionárias do comprimento, da largura e da altura.
Passo 1
Letra a) Vamos calcular a área do retângulo considerando o que pode variar, o retângulo tem lados que pode variar e que pode variar de , se a gente fizer a diferença da maior área com a menor, teremos uma boa estimativa para a incerteza.
Área máxima:
Área mínima:
Os termos foram omitidos, pois o enunciado falou que são termos desprezíveis.
Separando os termos em comum das incertezas temos que:
Podemos reescrever então a área do retângulo da seguinte forma:
Onde é a área dos lados conhecidos e é a incerteza.
Assim, chegamos ao que o enunciado pediu:
Passo 2
Letra b) Esse enunciado até embola um pouco a cabeça né? Quando ele fala de incerteza fracionária na área tá falando pra gente dividir a incerteza da área pela área conhecida, e provar que isso vale pras incertezas de comprimento, vamos ver se vale?
Vamos separar as frações aqui e pra ver se sai algo:
Logo, a incerteza fracionária na área é igual à soma das incertezas fracionárias do comprimento e da largura.
Passo 3
Letra c) Para achar a incerteza do volume o cálculo é similar. Cada um dos termos pode variar de incerteza, vamos calcular aqui o máximo e o mínimo e fazer a diferença o que nos dará a incerteza do volume.
Lembre-se de omitir todos os termos que são desprezíveis (todos onde temos duas incertezas multiplicadas).
Os termos desprezíveis são , , e .
Agora para o volume mínimo.
Os termos desprezíveis são , , e .
Logo, o volume com seu erro será:
Fazendo o cálculo da incerteza fracionária, teremos:
Resposta
Ei, a resposta está no passo a passo :)