12.39. Uma esfera sólida, uniforme, de massa igual a 1000 kg, possui um raio de 5,0 m. (a) Ache a força gravitacional que essa casa exerce sobre uma massa pontual de 2,0 kg colocada nas seguintes distâncias do centro da casca: (i) 5,01 m, (ii) 2,50 m. (b) Desenhe um gráfico qualitativo do módulo da força gravitacional que essa esfera exerce sobre uma massa pontual m em função da distância r de m do centro da esfera. Inclua a região de r=0 a
Passo 1
Vamos começar resolvendo o item (a). Bom a esfera tem e no caso (i), a massa pontual está a uma distância , então , logo, essa força gravitacional pode ser calculada como se calcula duas massas pontuais a uma distância
Agora é só substituir os valores
Fazendo essa continha
Passo 2
Agora vamos calcular para o caso (ii). Bem agora , então , mas como a esfera é sólida, então . Nesse caso a gente tem que lembrar que a massa M pode ser entendida com a sobreposição de infinitas cascas de esfera. Como a massa pontual está em , então toda parte da esfera sólida acima desse ponto, a gente desconsidera para o calculo da força, ou seja, a massa M da esfera sólida para o calculo dessa força é menor.
Um jeito simples que a gente pode calcular a massa da nova esfera, é pela densidade. A esfera que está interagindo agora tem metade do raio da esfera de mas a mesma densidade. Então podemos calcular a densidade
Lembra como calcula o volume de uma esfera?
Então
E também sabemos que
Então
Vamos colocar o volume em função do raio
A gente pode cortar várias coisas nessa equação
Agora substituindo os valores
Isso dá
Passo 3
Temos tudo para calcular a força gravitacional
Substituindo os valores
Fazendo essa continha
Passo 4
Agora vamos desenhar o gráfico. Vamos ver como o gráfico se comporta nos pontos em que . O calculo da força fica assim
Mas a massa também depende de , então
Isso vai dar
Ou seja, o gráfico se comporta como uma reta, com coeficiente angular .
Agora vamos ver nos pontos em que .
Nesses pontos podemos calcular a força como
Então nesses pontos a função é do tipo
Então fica algo parecido com isso
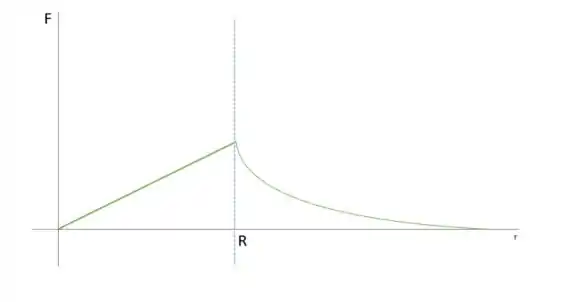
Resposta
b)