Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 73

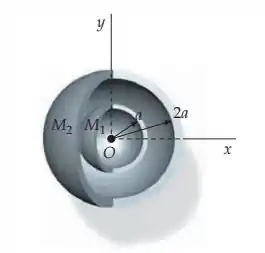
Duas cascas esféricas finas, homogêneas e concêntricas, possuem massas M 1 e M 2 e raios a   e 2 a , como na figura. Qual é a magnitude da força gravitacional sobre uma partícula pontual de massa m (não mostrada) localizada (a) a uma distância 3 a do centro das cascas? (b) a uma distância 1,9 a do centro das cascas? (c) a uma distância 0,9 a   do centro das cascas?

Passo 1

Pessoal, quando tiver casca esférica é mole! Dentro da casca não tem força gravitacional gerada por ela, e da superfície em diante a força gravitacional é escrita como:

F = G M m r 2

Passo 2

  1. Nessa distância, a massa é externa em relação às duas cascas, então as duas vão contribuir para a gravidade.

    2. F 3 a = G M 1 + M 2 m 3 a 2

    F 3 a = G M 1 + M 2 m 9 a 2

    Passo 3

  2. Nesse caso, a massa é externa em relação à casca menor, e interna em relação à casca maior, e essa não vai gerar campo sobre a massa, só a mais interna. Então, a força vai ser:

    3. F 1.9 a = G M 1 m 1.9 a 2

    F 1.9 a = G M 1 m 3.61 a 2

    Passo 4

  3. Nessa distância, a massa é interna às duas cascas. Então, a força gravitacional nela vai ser nula!

F 0.9 a = 0

Resposta

  1. F 3 a = G M 1 + M 2 m 9 a 2
  2. F 1.9 a = G M 1 m 3.61 a 2
  3. F 0.9 a = 0
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto no equador da Terra é acelerado (a) em direção ao centro da Terra porque a Terra gira em torno de si mesma, (b) em direção ao Sol porque a Terra gira em torno do Sol em uma órbita quase circ
Uma esfera maciça homogênea de raio R produz uma aceleração gravitacional a g na superfície. A que distância do centro da esfera está o ponto (a) do lado de dentro e (b) do lado de fora da esfera no q
Estrelas de nêutrons, como a que se localiza no centro da Nebulosa do Caranguejo, têm aproximadamente a mesma massa que nosso Sol, mas um diâmetro muito menor. Se você pesasse 675 N na Terra, qual ser
Um planeta na órbita de uma estrela distante possui raio de 3,24 X 106 m. A velocidade de escape para um objeto lançado da superfície desse planeta é de 7,65 × 10 3m / s . Qual é a aceleração da gravi
Um satélite terrestre move-se em uma órbita circular com uma velocidade orbital de 6.200m / s . Determine (a) o tempo de uma revolução do satélite; (b) a aceleração radial do satélite em sua órbita.