15. Para o circuito - do Exercício , faça um gráfico de , e contra para até . A corrente é dada por , logo, . Quais são os valores de , e para ? Compare o valor de com o de nesse instante. Repita a parte para .
Passo 1
Vamos lembrar as informações importantes que recebemos e chegamos do exercício pois elas serão extremamente úteis na nossa resolução.
Agora podemos prosseguir com nossa resolução.
Passo 2
Para montar o gráfico precisamos da equação de , e .
Vamos começar com
Nosso gráfico ficará:
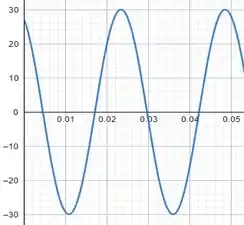
Passo 3
Agora vamos fazer para
O nosso gráfico fica:
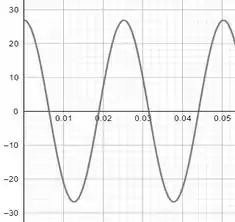
Passo 4
Para finalizar esse item e enfim juntar todos os gráficos vamos fazer o .
E o nosso gráfico é:
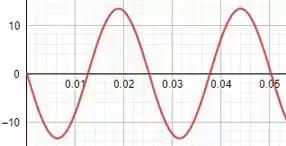
Passo 5
Vamos pegar todas as 3 equações anteriores e substituir pelo valor que o enunciado nos dá:
O valor de é um valor extremamente próximo ao valor de , podemos até dizer que
Passo 6
Repetindo os mesmos passos que no item anterior.
O valor de é exatamente o valor de , podemos dizer que
Resposta
Para :
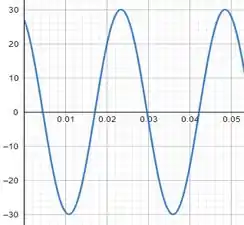
Para :
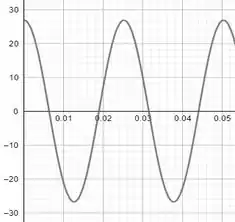
Para :
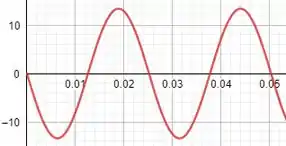
O valor de é um valor extremamente próximo ao valor de , podemos até dizer que
O valor de é exatamente o valor de , podemos dizer que