Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Problemas - Ex. 45
45. Um circuito para fazer derivadas. A corrente que passa em indutor sem resistência é indicada em função do tempo pelo gráfico da Figura . Faça um gráfico da configuração que se dever observar na tela de um osciloscópio conectado aos terminais do indutor. (O ponto luminoso do osciloscópio varre horizontalmente a tela com uma velocidade constante e sua deflexão vertical é proporcional à diferença de potencial entre os terminais do indutor.) Por que o indutor pode ser usado para obter um ‘circuito para fazer derivadas’?
Passo 1
Primeiro vamos tentar entender como ficaria mais o menos o gráfico que veremos no osciloscópio que como foi dito no enunciado é um gráfico .
O enunciado nos fornece um gráfico , então temos que relacionar a corrente de um indutor com a voltagem, isso pode ser feito através da seguinte fórmula:
Então o que a eletrônica do osciloscópio faz é calcular a derivada do gráfico .
Então as partes do gráfico da corrente que estão subindo ou descendo quando derivadas representam retas constantes, logo voltagem constante e os bicos do gráfico representam pontos onde temos quedas ou subidas repentinas na voltagem já que a derivada na região dos bicos não é bem definida.
Passo 2
Levando em conta as observações feitas no item anterior, o gráfico fica mais ou menos no formato abaixo.
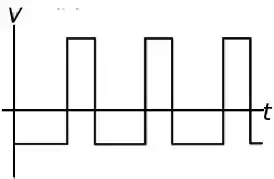
Passo 3
A resposta do item tem a ver com o que foi dito mais acima. O que o osciloscópio mostra na tela é bem dizer a derivada do que ele está medindo, mas como um equipamento eletrônico vai pegar e realizar a derivada?
Não tem como então por isso temos o indutor, ele meio que o componente que realiza essa derivada por conta de seu comportamento, ele fornece um resultado de tenção quando tem uma corrente passando por ele que é justamente igual a derivada da função dessa mesma corrente.
Resposta
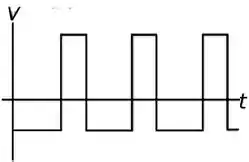
Ele fornece um resultado de tenção quando tem uma corrente passando por ele que é justamente igual a derivada da função dessa mesma corrente.