Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 23.Exercícios - Ex. 54
Cargas puntiformes idênticas, , são colocadas em ângulos opostos de um quadrado, cujo lado possui comprimento igual a . O ponto A está em um dos ângulos
vazios e o ponto está no centro do quadrado. Uma carga puntiforme é colocada no ponto e se desloca ao longo da diagonal do quadrado até o ponto . Qual é o módulo da força elétrica resultante sobre quando ela está no ponto ? Faça um desenho com as localizações das cargas e a direção e o sentido da força resultante. Qual é o módulo da força elétrica resultante sobre quando ela está no ponto ? Qual é o trabalho realizado pela força elétrica sobre durante seu deslocamento de até ? Esse trabalho é positivo ou negativo? Quando se desloca de até , ela se aproxima de um potencial mais alto ou mais baixo?
Passo 1
Vem comigo que a gente resolve essa juntos!
Primeiro vamos representar nossa situação, as cargas estão distribuídas da seguinte forma:
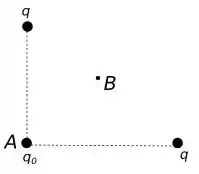
Pelas informações do enunciado a carga tem sinal oposto as cargas logo a força entre as cargas é de atração.
Só que cada carga atrai para si, então temos que a força resultante tem a seguinte direção:
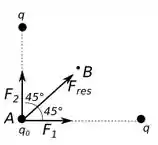
Então o módulo da força resultante no ponto é:
Como as cargas são iguais, temos que:
Agora quando a carga está em as forças que as cargas fazem em são opostos, sabendo disso podemos calcular a força resultante nesse ponto.
Para acharmos o trabalho feito pela força podemos usar a seguinte equação:
Como é a partícula que se move, temos:
E vamos usar também que:
Vamos as contas então!
Passo 2
Começando com o item .
Temos que a força resultante é dada por:
Usando a expressão que vimos no passo para e , temos:
Substituindo com os valores que conhecemos, temos:
Então temos que:
Passo 3
Agora o item .
Como falamos no passo no ponto as forças que cada carga faz em são opostas e como:
Temos que a força resultante em é zero.
Passo 4
Agora para o item , temos o seguinte:
E sabendo que:
`Podemos juntar tudo e ficamos com:
Temos que e já que o ponto fica no centro do quadrado e a distância desse ponto as cargas é metade da diagonal do quadrado.
Então temos que:
Assim temos que:
Temos um trabalho positivo, então a carga se aproxima de um potencial mais alto.