Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 63
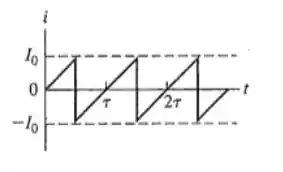
63 - A corrente em um circuito varia com o tempo como indicado na Figura 31.28. Calcule a corrente média e o valor eficaz (ou valor quadrático médio) da corrente em termos de .
Passo 1
Ora, perceba que a função é periódica de período (é a retinha de até que se repete todo o tempo)!
Precisamos descrever essa função corrente, para isso vamos descrever a retinha que vai de até . Para uma reta, precisamos de 2 pontos:
Precisamos de pontos conhecidos para determinar o valor de e . No nosso caso os pontos são os de extremo da retinha:
Então...
Multiplicando a de cima por e somando as duas equações...
Quanto ao ...
Então a nossa retinha é...
Passo 2
Ora, a corrente média é definida como sendo...
Onde é o valor do período da nossa função, onde no nosso caso e . Mas no nosso caso, nem precisamos calcular, pois pelo desenho dá para perceber que...
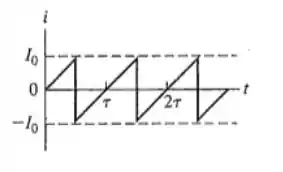
De a , a função está perfeitamente simétrica em relação ao eixo que passa por , de modo que quando integrarmos vamos obter :
Passo 3
Já para obter o valor eficaz...
E agora o resultado deixa de ser já que estamos integrando e não mais (o gráfico de não tem partes negativas). Logo, substituindo...
Se fizermos a substituição...
Então...
Substituindo os limites...
Portanto, o valor de RMS é...
Resposta
Ei, a resposta está no passo a passo :)