Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 63
63. Um pêndulo consiste de um bastão rígido e de massa desprezível com uma massa em uma das extremidades. A outra extremidade é presa a um eixo sem atrito de modo que possa girar e completar uma volta. O pêndulo é invertido e, então, quando a massa se encontra verticalmente acima do pino, é liberado. A velocidade da massa ao passar pelo ponto mais baixo é de . Se o pêndulo efetuar oscilações de pequena amplitude na parte inferior do arco circular, qual será a freqüência?
Passo 1
Opa! E aí brother! Aqui vamos nós de novo!
Se liga só! A primeira coisa que devemos fazer, é um esboço pra representar melhor o que está acontecendo, inclusive posicionando um referencial pra ficar do jeito mais claro possível.
E aqui está nossa bela figura...
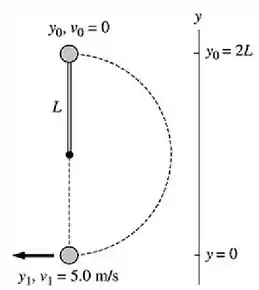
Passo 2
Aí já sabe o que tem que fazer, né companheiro!?
Partiu usar a conservação da energia mecânica
Onde é a notação pra quando nossa massa está na altura e pra quando ela está na origem.
E ficamos então, com...
Sabendo que a velocidade da massa ao passar pelo ponto mais baixo em é de , o comprimento vai ser de...
Passo 3
Finalmente, para obter a frequência de oscilação, basta usar a fórmula abaixo para oscilação em um sistema pendular:
Como já sabemos o valor de , então...
Pronto! Essa é a nossa frequência do pêndulo!