Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 65

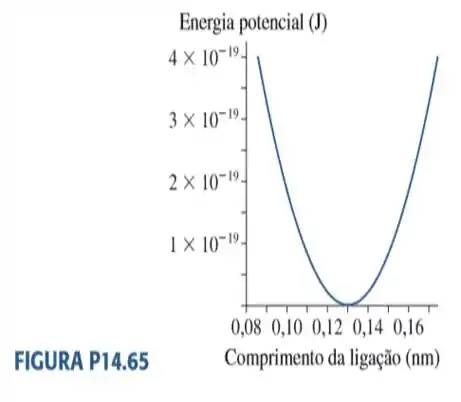
65. Uma ligação molecular pode ser modelada como uma mola presa entre dois átomos que vibram em movimento harmônico simples. A FIGURA P14.65 mostra uma aproximação de MHS para a energia potencial de uma molécula de H C l . Para E < 4 ⋅ 10 19   J J, esta é uma boa aproximação para a curva mais precisa de energia potencial do H C l mostrada na Figura 10.37. Uma vez que o átomo de cloro possui massa muito maior do que o átomo de hidrogênio, é razoável presumir que o átomo de hidrogênio ( m =   1,67 ⋅ 10 27   k g ) vibra de um lado para o outro enquanto o átomo de cloro permanece praticamente em repouso. Use o gráfico abaixo para estimar a frequência vibracional da molécula de H C l .

Passo 1

Opa! E aí brother! Aqui vamos nós de novo!

Se liga só cumpadi! Pelo gráfico e pelo que lemos do enunciado, a melhor aproximação possível para trabalharmos com energia na nossa molécula, onde apenas os átomos de hidrogênio estão vibrando, é considerar nosso sistema como muito próximo a um modelo massa-mola...

E nesse modelo sabemos que a energia potencial para qualquer ponto, é dada por...

U = 1 2 k ( ∆ x ) 2

U = 1 2 k ( x - x 0 ) 2

Onde x é a notação pro comprimento da ligação.

E olhando novamente o gráfico do enunciado, podemos ver que no equilíbrio, o comprimento de ligação da molécula de H C l é dado por...

x 0 = 0,12   n m

Passo 2

Como não sabemos o valor da nossa constante k , já que nosso gráfico tem um monte de pontos; eis aqui uma bela sacada... Que tal pegarmos três valores do gráfico e vermos qual o valor da energia em cada um deles!

Pois é exatamente isso que vamos fazer!

Para x = 0,11   n m ...

U = 1 2 k ( x - x 0 ) 2

k = 2 U ( x - x 0 ) 2

k = 2 ⋅ 0,8 ⋅ 10 - 19   J ( 0,11   n m - 0,12   n m ) 2

k = 400   N / m

Para x = 0,10   n m ...

U = 1 2 k ( x - x 0 ) 2

k = 2 U ( x - x 0 ) 2

k = 2 ⋅ 1,9 ⋅ 10 - 19   J ( 0,10   n m - 0,12   n m ) 2

k = 422   N / m

Para x = 0,09   n m ...

U = 1 2 k ( x - x 0 ) 2

k = 2 U ( x - x 0 ) 2

k = 2 ⋅ 3,4 ⋅ 10 - 19   J ( 0,09   n m - 0,12   n m ) 2

k = 425   N / m

Sendo assim, montamos a seguinte tabela...

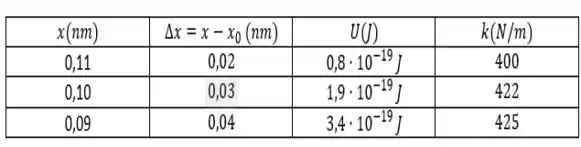
E pra obter a constante média, basta tirar a média dos valores de k ...

k m é d = 400   N / m + 422   N / m + 425   N / m 3

k m é d = 416   N / m

Passo 3

Pra finalizar, como aproximamos nossa molécula em um sistema massa-mola, então a fórmula da frequência será a mesma. Ela vai ser dada por...

f = 1 2 π k m

No caso, temos que...

f = 1 2 π k m é d m

f = 1 2 π 416   N / m   1,67 ⋅ 10 27   k g )  

f = 7,9 ⋅ 10 13   H z

Resposta

f = 7,9 ⋅ 10 13   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função velocidade v t aparece na figura se a função posição x ( t ) é da forma x = x m c o s ⁡ ( ω t + φ ) ? A escala do eixo vertical é definida
Qual é a constante de fase do oscilador harmônico cuja função posição x ( t ) aparece na figura se a função posição é da forma x = x m c o s ⁡ ( ω t + φ ) ? A escala do eixo vertical é definida por x
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A Fig. 15-51 mostra a posição x t de um bloco que oscila em um MHS na extremidade de uma mola t s = 40,0 m s . Qual é (a) a velocidade e (b) o módulo da aceleração radial de uma partícula no movimento
13.13E Considere as n raízes enésima da unidade, ou seja, as n soluções de z = 1 n , para A) n = 2 , B) n = 3 e C) n = 4 . Para cada valor de n , represente as soluções encontradas em um gráfico no pl