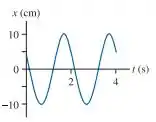
A FIGURA Q14.3 mostra um gráfico posição versus tempo para uma partícula em MHS. Quais são (a) a amplitude A, (b) a frequência angular e (c) a constante de fase do movimento? Explique
Passo 1
- A amplitude de um MHS é o valor máximo e mínimo de . Pelo gráfico, notamos que tais valores são e . Assim, a amplitude do movimento irá valer 10 s.
- A frequência angular pode ser calculada por:
- A equação do MHS é dada por:
Passo 2
onde é o período de oscilação. Para a gente obter , devemos verificar quanto tempo a partícula demora para passar pela mesma posição e indo para o mesmo sentido. Veja na figura abaixo:
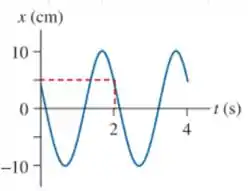
Veja que buscamos procurar em quanto tempo a partícula demora para passar e indo para a esquerda (indo para valores menores de ). Portanto, . Logo,
Passo 3
Para , temos:
No gráfico, notamos que para . Além disso, como vimos no item a. temos . Logo,
Assim, temos dois valores possíveis para :
- rad;
- rad.
Qual dos dois devemos escolher? Notemos que em a velocidade é negativa (já a partícula está indo para valores menores de ). Como:
segue que, para :
Dessa forma, para que , devemos ter (pois já temos o sinal negativo)
- ;
Assim, segue que devemos escolher rad!
Resposta
- .
- .
- .