Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Questões Conceituais - Ex. 5

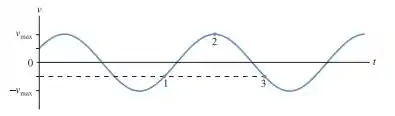
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS.

a. Quanto vale a constante de fase ϕ 0 ? Explique.

b. Qual é a fase da partícula em cada um dos três pontos, numerados no gráfico?

Passo 1

Sabemos que a velocidade de um corpo em MHS pode ser equacionada como:

v t = - v m á x sin ⁡ ω t + ϕ 0

A aceleração é obtida derivando a expressão acima, em relação ao tempo:

a t = - v m á x ω cos ⁡ ω t + ϕ 0

Passo 2

  1. A fase inicial, ϕ 0 , é obtida fazendo t = 0 nas equações apresentadas acima.

    2. Pelo gráfico, vemos que v 0 = v m á x / 2 . Logo,

    v 0 = - v m á x sin ⁡ ϕ 0 v m á x 2 = - v m á x sin ⁡ ϕ 0 sin ⁡ ϕ 0 = - 1 2

    Portanto, temos dois possíveis valores para ϕ 0 :

    1. ϕ 0 = 7 π / 6 ;
    2. ϕ 0 = 11 π / 6 .

    Como podemos decidir qual valor da fase inicial? Podemos pensar na aceleração! Em t = 0 , vemos que a velocidade está aumentando, sendo assim a 0 > 0 . Como:

    a 0 = - v m á x ω cos ⁡ ϕ 0

    Para que a 0 > 0 , devemos ter cos ⁡ ϕ 0 < 0 . Isso só será possível se escolhermos ϕ 0 = 7 π / 6 .

    Portanto, temos

    ϕ 0 = 7 π 6

    Passo 3

  2. A fase em um instante qualquer é ϕ = ω t + ϕ 0 .
  1. No ponto 1 , temos v = - v m á x / 2 . Logo,

    2. v = - v m á x sin ⁡ ω t + ϕ 0 - v m á x 2 = - v m á x sin ⁡ ϕ sin ⁡ ϕ = 1 2

    Assim, temos duas possibilidades para ϕ :

    1. ϕ = π / 6 ;
    2. ϕ = 5 π / 6 .

    Novamente, devemos olhar a aceleração. No ponto 1 , temos a > 0 (a velocidade está aumentando). Logo, como

    a = - v m á x ω cos ⁡ ϕ

    para que a > 0 , devemos ter cos ⁡ ϕ < 0 . Logo, a única escolha possível é 5 π / 6 .

  2. No ponto 2, temos v = v m á x . Logo,

    3. v = - v m á x sin ⁡ ω t + ϕ 0 v m á x = - v m á x sin ⁡ ϕ sin ⁡ ϕ = - 1

    Portanto, temos apenas uma possibilidade: ϕ = 3 π / 2 .

  3. No ponto 3, temos v = - v m á x / 2 e uma aceleração negativa. Portanto, das duas possibilidades que a gente encontrou no item 1, devemos escolher aquela que nos dá a aceleração negativa, ou seja, ϕ = π / 6 .

Resposta

  1. ϕ 0 = 7 π / 6 .
  2. ϕ 1 = 5 π / 6 ϕ 2 = 3 π / 2 ϕ 3 = π / 6
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto em movimento harmônico simples tem amplitude de 4,0 cm e frequência de 4,0 Hz e, em t = 0 s, passa pelo ponto de equilíbrio se movendo para a direita. Escreva a função x ( t ) que descreve a
Quais são a (a) amplitude, (b) frequência e (c) constante de fase da oscilação mostrada na FIGURA EX14.5?
60. Um deslizador de 250g sobre um trilho de ar é preso a uma mola de constante elástica4,0N / m . A constante de amortecimento devido à resistência do ar vale 0,015k g / s . O carrinho é deslocado 20
59. Uma argola circular de massa M e raioR é pendurada a um eixo, conforme mostra a FIGURA P 14.59 . Obtenha uma expressão para a freqüência de pequenas oscilações.
62. Um bloco de 200g , preso a uma mola horizontal, oscila com amplitude de 2,0c m e freqüência de 2,0H z . Exatamente quando ele está passando pelo ponto de equilíbrio, movendo-se para a direita, um