67. Uma moeda de centavo encontra-se sobre o topo de um pistão enquanto efetua um movimento harmônico simples com de amplitude. Se a freqüência for baixa, a moeda sobe e desce sem dificuldade. Se a freqüência for gradualmente aumentada, chega um momento em que a moeda perde contato com a superfície do pistão.
a. Em que ponto do ciclo a moeda perde contato com o pistão pela primeira vez?
b. Qual é a frequência máxima possível se a moeda deve permanecer sobre o pistão durante o ciclo inteiro?
Passo 1
Opa! E aí brother! Aqui vamos nós de novo!
Se liga só! A primeira coisa que devemos fazer, é um esboço pra representar melhor o que está acontecendo
E aqui está nossa bela figura...
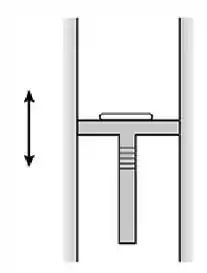
Em seguida, bora fazer o diagrama de corpo livre para a moeda, representando as forças que estão atuando nela...
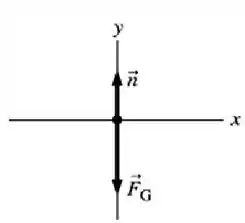
Passo 2
Aí já sabe o que tem que fazer, né companheiro!?
Partiu usar a segunda lei de Newton pro eixo ...
Agora foco nesse relação!
Se a força resultante, , está para cima na parte inferior do ciclo (positivo), isso só pode significar uma coisa...
A velocidade é máxima ao passar pelo ponto de equilíbrio! E como todo , sabemos que nesse ponto a resultante das forças é nula e não há aceleração. Logo e também...
O ponto crítico é o ponto mais alto. aponta para baixo e é negativo. Se se tornar suficientemente negativo, a normal cai para zero e a moeda não está mais em contato com a superfície. Esse é o ponto do ciclo em que a moeda perde contato com o pistão pela primeira vez
Passo 3
Bem! Pelo exemplo anterior, vimos que há um ponto na oscilação onde a moeda perde contato com o pistão e nesse ponto a normal vale zero...
Sendo assim, como só temos força gravitacional agindo nesse instante, a única possibilidade da moeda não sair do pistão é que sua aceleração seja igual a da gravidade, em sentido contrário pra rivalizar com a força peso.
Logo;
E como sabemos que a aceleração é o produto da amplitude pelo quadrado da frequência angular...
E sabendo também da outra fórmula abaixo que relaciona com a frequência em ;
Finalmente obtemos a frequência angular máxima possível para a moeda permanecer sobre o pistão durante toda a oscilação.