Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 5

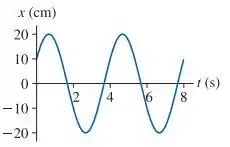
Quais são a (a) amplitude, (b) frequência e (c) constante de fase da oscilação mostrada na FIGURA EX14.5?

Passo 1

Podemos modelar a posição de um corpo em MHS da seguinte forma:

x t = A cos ⁡ ω t + ϕ 0

onde A é a amplitude, ω é a frequência angular e ϕ 0 é a fase inicial.

Passo 2

  1. A amplitude será os máximos valores de x . Pelo gráfico, vemos que a amplitude é de 20   c m .

    2. Passo 3

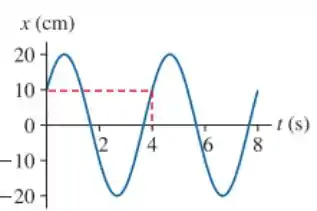
  2. Veja a figura abaixo.

    3. Note que em t = 0 a partícula está em x = 10   c m e está indo para a direita (valores maiores de x ). Apenas em t = 4   s a partícula passa novamente por x = 10   c m indo para a direita. Assim, o período vale T = 4,0   s . A frequência poderá ser calculada por:

    f = 1 T f = 1 4,0 f = 0,25   H z

    Passo 4

  3. A constante de fase é obtida para t = 0 . Assim,

x 0 = A cos ⁡ ω ⋅ 0 + ϕ 0 x 0 = A cos ⁡ ϕ 0

Pelo gráfico, vemos que x 0 = + 10   c m . Logo,

10 = 20 cos ⁡ ϕ 0 cos ⁡ ϕ 0 = 0,5

Portanto, temos dois possíveis valores para ϕ 0 :

  1. ϕ 0 = π / 3 .
  2. ϕ 0 = 5 π / 3 .

Como decidir qual ϕ 0 é o correto? Vamos olhar para a velocidade! Note que em t = 0 a velocidade deve ser positiva (pois x está aumentando). Como:

v t = - A ω sin ⁡ ω t + ϕ 0 v 0 = - A ω sin ⁡ ϕ 0

Logo, para que v 0 > 0 , devemos ter sin ⁡ ϕ 0 < 0 , o que só é possível se tivermos ϕ 0 = 5 π / 3 .

Resposta

  1. A = 20   c m .
  2. f = 0,25   H z .
  3. ϕ 0 = 5 π 3   r a d .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 15-51 mostra a posição x t de um bloco que oscila em um MHS na extremidade de uma mola t s = 40,0 m s . Qual é (a) a velocidade e (b) o módulo da aceleração radial de uma partícula no movimento
Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
17. Sobre um trilho de ar sem atrito, horizontal, um corpo oscila na extremidade de uma mola ideal de constante 2,50N / c m . O gráfico da Figura 13.31 mostra a aceleração do corpo em função do tempo.
Ache o movimento resultante de dois movimentos harmônicos simples na mesma direção dados por: x 1 = cos ⁡ ω t - π 6 , x 2 = sen ⁡ ω t . Represente graficamente os respectivos vetores girantes.
Trace as figuras de Lissajous corerespondentes à composição dos seguintes movimentos harmônicos simples em direções perpendiculares:(a) x = A cos ⁡ ω t , y = A sen ⁡ 2 ω t .(b) x = A sen ⁡ ω t , y = A