Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 6

Um objeto em movimento harmônico simples tem amplitude de 4,0 cm, frequência de 2,0 Hz e constante de fase de 2 π / 3 rad. Desenhe um gráfico de posição mostrando dois ciclos do movimento.

Passo 1

Sabemos que a posição de um corpo em MHS pode ser modelada como:

x = A cos ⁡ ω t + ϕ 0

onde A é a amplitude, ω é a velocidade angular e ϕ 0 é a fase inicial. Pelos dados do problema, temos que A = 4,0   c m , f = 2 , 0   H z e ϕ 0 = 2 π / 3 . Para calcular ω , lembremos da relação:

ω = 2 π f ω = 2 π 2,0 ω = 4 π   r a d / s

Logo, temos

x t = 4,0 cos ⁡ 4 π t + 2 π 3

Passo 2

Devemos desenhar o gráfico da função acima. Veja a figura abaixo e as respectivas explicações.

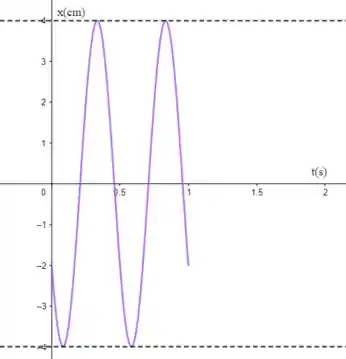
Note que, em t = 0 , temos:

x 0 = 4 cos ⁡ 2 π 3 x 0 = 4 - 0,5 x 0 = - 2   c m

Além disso, a velocidade é dada por:

v t = - 16 π sin ⁡ 4 π t + 2 π 3 v 0 = - 16 π sin ⁡ 2 π 3 v 0 = - 8 π 3   m / s

ou seja, a velocidade é negativa em t = 0 . Por isso o gráfico começa em x = - 2   c m e vai descendo até x = - 4   c m que é o ponto de mínimo. Além disso, o período deve ser:

T = 1 f = 1 2 = 0,5   s

Portanto, a cada 0,5 s tudo deve se repetir!

Resposta

Ver gráfico acima.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS. a. Qual é a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos numerados no grá
A FIGURA Q14.3 mostra um gráfico posição versus tempo para uma partícula em MHS. Quais são (a) a amplitude A, (b) a frequência angular ω e (c) a constante de fase ϕ 0 do movimento? Explique
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad
13.2E O movimento de um oscilador harmônico é descrito por x = 0,75cm. cos ⁡ ( 5,0t/s ) - 0,40cm. sen ⁡ 5,0t/s . Escreva este movimento na forma de x = x m cos ⁡ ω t + ϕ .
13.11E Calcule o módulo dos números: z 1 = 4,0 + 3,0 i ,z 2 = 15 e i ϕ ,z 3 = 20 i cos ⁡ 30 ° + sin ⁡ 60 ° .