Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.3 - Ex. 30
Algumas pedras rolando aproximam-se da base de uma colina com uma velocidade de . A colina está inclinada em acima do plano horizontal e possui coeficientes de atrito cinético e estático de e , respectivamente, com essas pedras. (a) Ache a aceleração das pedras enquanto elas deslizam até a colina. (b) Quando uma pedra alcança seu ponto mais alto, ela permanecerá ali ou deslizará colina abaixo? Se permanecer, mostre por quê. Se descer, ache sua aceleração no caminho de retorno.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar (a) a aceleração das pedras quando elas deslizam até a colina e (b) verificar o que acontece quando uma pedra alcança seu ponto mais alto.
A segunda lei de Newton se aplica às pedras na colina. Quando estão em movimento, o atrito cinético age sobre elas, mas quando estão em repouso, o atrito estático age.
Então, vamos usar as coordenadas com eixos paralelos e perpendiculares à inclinação, com na direção da aceleração para calcular as forças conforme a segunda lei na forma:
Vamos lá!
Passo 2
a) Com a pedra está deslizando morro acima, a força de atrito é descendo a colina e diagrama de corpo livre é dado na figura (a):
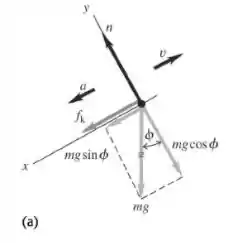
Calculando as forças na direção vertical, usando a segunda lei de Newton, temos:
Onde representa a força de contato e a componente da força peso na direção . Sendo assim, com a força de atrito estático dada por:
Vamos ter:
Passo 3
Agora na direção horizontal, vamos ter:
Onde é a componente horizontal da força peso e a componente horizontal da força de atrito.
Então, isolando a aceleração na equação, temos:
E substituindo os valores, obtemos:
Passo 4
b) O componente da gravidade no declive é . A força de atrito estática máxima é:
Então,
Portanto, não pode ser tão grande quanto e a pedra desliza pra baixo.
Conforme a pedra desliza para baixo, a força sobe a inclinação. O diagrama de corpo livre é dado na figura (b).
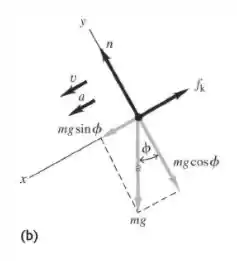
Assim, fazendo o somatório de forças verticais, teremos:
Logo, a força de atrito será dada por:
E na direção horizontal, teremos:
Então, isolando na equação:
Para baixo.
A aceleração descendo a inclinação em (a) é maior do que em (b) porque em (a) o atrito estático e a gravidade atuam na inclinação, enquanto em (b) o atrito está na inclinação, opondo-se à gravidade que ainda atua na inclinação.
Valeu, galera! Até a próxima! 😉