Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 3.Exercícios e Problemas - Ex. 6
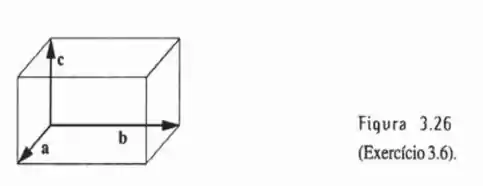
As arestas do paralelepípedo visto na Figura 3.26 são mutuamente perpendiculares. Mostre que o produto misto é igual ao volume do paralelepípedo.
Passo 1
Meus fofinhos, para saber o produto misto dos 3 vetores, precisamos saber as coordenadas de cada um!!!
Portanto, é dado por:
Calculando o determinante, temos que:
Que resulta no volume do paralelepípedo!!!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
No Capítulo 8, introduziremos um novo vetor associado a uma partícula, a sua quantidade de movimento linear, simbolizado por p → . Matematicamente, ele está relacionado à massa m e à velocidade v → da
Os vetores unitários A ^ e B ^ estão no plano xy. Eles formam os ângulos θ 1 e θ 2 , respectivamente, com o eixo +x. (a) Use trigonometria para encontrar diretamente as componentes x e y dos dois veto
(a) Seja A → um vetor constante, no plano xy, com sua origem na origem do sistema de coordenadas. Seja r → = x i ^ + y j ^ um vetor do plano xy que satisfaz à relação A → ∙ r → = 1 . Mostre que os pon
Uma partícula se move em um círculo centrado na origem, a magnitude de seu vetor posição r → sendo constante. (a) Derive r → ∙ r → = r 2 = c o n s t a n t e em relação ao tempo, para mostrar que v → ∙
Dois vetores aeb são tais que a + b = a - b . Qual é o ângulo entre aeb ?