Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 83
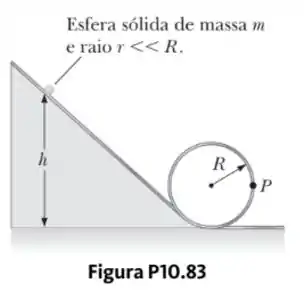
Uma esfera sólida de massa e raio rola sem escorregar ao longo da pista mostrada na Figura P10.83. Ela começa do repouso com o ponto mais baixo da esfera na altura acima da base do aro de raio , muito maior que .
- Qual é o valor mínimo de (quanto ao ) para que a esfera complete o aro?
- Quais são as componentes da força da esfera no ponto se ?
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
A conservação de energia nos dá:
Para uma esfera:
Observe que quando a velocidade da esfera no topo do loop satisfaz a condição
Substituindo isso na equação [1] dá:
Passo 2
Letra b:
Quando a esfera está inicialmente em e finalmente no ponto P, a conservação de energia nos dá:
Em y temos:
Resposta
Exercícios de Livros Relacionados
Uma casca esférica uniforme de 8,40 kg e 50,0 cm de diâmetro possui quatro pequenas massas de 2,0 kg presas à superfície externa e igualmente espaçadas entre si. Esse sistema está girando em torno de
Um balde com água de 15,0k g é suspenso por uma corda enrolada em torno de um sarilho, constituído por um cilindro sólido com diâmetro de 0,300m e massa igual a 12,0k g . O cilindro é pivotado sobre u
A peça de uma máquina tem o formato de uma esfera maciça e uniforme com massa de 225 g e diâmetro de 3,0 cm. Ela está girando em torno de um eixo com atrito desprezível que passapelo seu centro, mas e
Um cilindro maciço e uniforme com massa de 8,25k g e diâmetro de 15,0c m está girando a 220r p m sobre um eixo delgado e de atrito desprezível, que passa ao longo do eixo de cilindro. Você projeta um
Um poste delgado e uniforme de 15,0 kg e 1,75 m de comprimento é mantido na posição vertical por um cabo e está preso a uma massa de 5,0 kg e um pivô na sua extremidade inferior(Figura 10.45). O fio p